练习册

  • 练习册
  • 试题
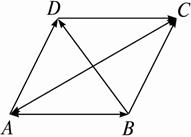
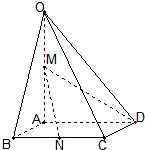    精英家教网 > 高中数学 > 题目详情
    如图2-2-4，四边形ABCD为菱形，则下列等式中成立的是(    )

    图2-2-4

    A.              B.

    C.              D.

    解析：由三角形法则和平行四边形法，可知,A错；，B错；，D错.只有C是正确的.

    答案：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，∠ABC=
    π4
    ，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．
    （Ⅰ）证明：直线MN∥平面OCD；
    （Ⅱ）求异面直线AB与MD所成角的大小；
    （Ⅲ）求点B到平面OCD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

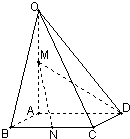    如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，∠ABC=
    π4
    ，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．
    （Ⅰ）证明：直线MN∥平面OCD；
    （Ⅱ）求异面直线AB与MD所成角的大小；
    （Ⅲ）求二面角A-OD-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

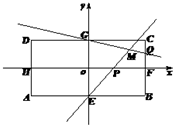    如图，在矩形ABCD中，AB=8，BC=4，E，F，G，H分别为四边的中点，且都在坐标轴上，设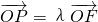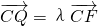数学公式，数学公式（λ≠0）．
    （Ⅰ）求直线EP与GQ的交点M的轨迹Γ的方程；
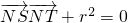    （Ⅱ）过圆x2+y2=r2（0＜r＜2）上一点N作圆的切线与轨迹Γ交于S，T两点，若数学公式，试求出r的值．

    查看答案和解析>>

    科目：高中数学 来源：2012年浙江省温州市高考数学一模试卷（理科）（解析版） 题型：解答题

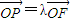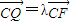    如图，在矩形ABCD中，AB=8，BC=4，E，F，G，H分别为四边的中点，且都在坐标轴上，设，（λ≠0）．
    （Ⅰ）求直线EP与GQ的交点M的轨迹Γ的方程；
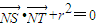    （Ⅱ）过圆x2+y2=r2（0＜r＜2）上一点N作圆的切线与轨迹Γ交于S，T两点，若，试求出r的值．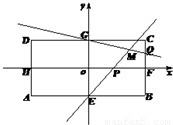

    查看答案和解析>>

    科目：高中数学 来源：2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷19（理科）（解析版） 题型：解答题

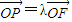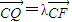    如图，在矩形ABCD中，AB=8，BC=4，E，F，G，H分别为四边的中点，且都在坐标轴上，设，（λ≠0）．
    （Ⅰ）求直线EP与GQ的交点M的轨迹Γ的方程；
    （Ⅱ）过圆x2+y2=r2（0＜r＜2）上一点N作圆的切线与轨迹Γ交于S，T两点，若，试求出r的值．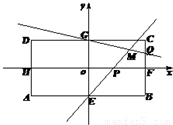

    查看答案和解析>>

    同步练习册答案