
已知椭圆![]() =1(a>b>0)的离心率
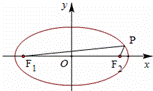
=1(a>b>0)的离心率![]() ,且短半轴b=1,F1,F2为其左右焦点,P是椭圆上动点.
,且短半轴b=1,F1,F2为其左右焦点,P是椭圆上动点.
(Ⅰ)求椭圆方程.
(Ⅱ)当∠F1PF2=60°时,求△PF1F2面积.
(Ⅲ)求![]() 取值范围.
取值范围.
考点:
圆锥曲线的综合.
专题:
圆锥曲线的定义、性质与方程.
分析:
(Ⅰ)利用椭圆![]() =1(a>b>0)的离心率
=1(a>b>0)的离心率![]() ,且短半轴b=1,建立方程组,求出几何量,即可求椭圆方程.
,且短半轴b=1,建立方程组,求出几何量,即可求椭圆方程.
(Ⅱ)当∠F1PF2=60°时,利用余弦定理,求出|PF1||PF2|,再利用三角形面积公式,可求△PF1F2面积.
(Ⅲ)用坐标表示向量,再利用数量积公式,即可求![]() 取值范围.
取值范围.
解答:
解:(Ⅰ)∵椭圆![]() =1(a>b>0)的离心率
=1(a>b>0)的离心率![]() ,且短半轴b=1,
,且短半轴b=1,
∴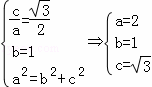
∴椭圆方程为![]() …(4分)
…(4分)
(Ⅱ)设|PF1|=m,|PF2|=n,
∵![]() ,
,
∴在△PF1F2中,由余弦定理得:![]() =12=m2+n2﹣2mncos60°=m2+n2﹣mn=(m+n)2﹣3mn=16﹣3mn
=12=m2+n2﹣2mncos60°=m2+n2﹣mn=(m+n)2﹣3mn=16﹣3mn
∴![]() …(7分)
…(7分)
∴![]() …(9分)
…(9分)
(Ⅲ)设P(x0,y0),则![]() ,即
,即![]()
∵![]() ,∴
,∴![]()
∴![]() …(11分)
…(11分)
∵﹣2≤x0≤2,∴![]()
故![]() …(13分)
…(13分)
点评:
本题考查椭圆的方程,考查余弦定理的运用,考查向量数量积公式,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2009-2010学年湖北省武汉市六校高三(上)第一次联考数学试卷(文科)(解析版) 题型:填空题
 +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 .查看答案和解析>>
科目:高中数学 来源:2012年安徽省合肥八中高考数学一模试卷(文科)(解析版) 题型:解答题
 +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 .查看答案和解析>>
科目:高中数学 来源:2010年河南省高二上学期12月份考试数学卷(文理) 题型:解答题
(12分)如图,已知椭圆 =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 ,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
,左、右焦点分别为F1、F2. 点P为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点.
(1)求椭圆的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2, 证明: =2;
=2;
查看答案和解析>>
科目:高中数学 来源:2010年河南省高二上学期12月份考试数学卷(文理) 题型:选择题
已知椭圆 =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为
A、 B、
B、 C、
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com