已知函数f(x)＝mx3－3(m＋1)x2(3m＋6)x＋1，其中m∈R，m＜0，
(1)若m＝－2，求y＝f(x)在(2，–3)处的切线方程；
(2)当x∈[－1，1]时，函数y＝f(x)的图象上任意一点的切线斜率恒大于3m，求m的取值范围．
科目：高中数学 来源：2013-2014学年宁夏高三上学期第五次月考理科数学试卷（解析版） 题型：解答题
已知函数f(x)＝m－|x－2|，m∈R，且f(x＋2)≥0的解集为[－1,1]．
（1）求m的值；
（2）若a，b，c∈R＋，且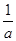
＋
＋
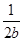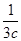＝m，求证：a＋2b＋3c≥9.
查看答案和解析>>
科目：高中数学 来源：2012届江西省南昌市高三第一次模拟测试卷理科数学试卷 题型：解答题
已知函数f(x)＝
(m，n∈R)在x＝1处取到极值2.
(1)求f(x)的解析式；
(2)设函数g(x)＝ax－lnx.若对任意的x1∈[
，2]，总存在唯一的x2∈[
，e](e为自然对数的底)，使得g(x2)＝f(x1)，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源：2010年宁夏高二上学期期中考试数学卷 题型：解答题
（本小题满分12分）
已知函数f(x)＝m·2x＋t的图象经过点A(1,1)、B(2,3)及C(n，Sn)，Sn为数列{an}的前n项和，n∈N*.
(1)求Sn及an；
(2)若数列{cn}满足cn＝6nan－n，求数列{cn}的前n项和Tn.
查看答案和解析>>
科目：高中数学 来源： 题型：
（本小题满分12分）
已知函数f(x)＝m·2x＋t的图象经过点A(1,1)、B(2,3)及C(n，Sn)，Sn为数列{an}的前n项和，n∈N*.
(1)求Sn及an；
(2)若数列{cn}满足cn＝6nan－n，求数列{cn}的前n项和Tn.
查看答案和解析>>
科目：高中数学 来源：江西省南昌市2011-2012学年高三下学期第一次模拟测试卷（数学理） 题型：解答题
已知函数f(x)＝(m，n∈R)在x＝1处取到极值2.
(1)求f(x)的解析式；
(2)设函数g(x)＝ax－lnx.若对任意的x1∈[，2]，总存在唯一的x2∈[，e](e为自然对数的底)，使得g(x2)＝f(x1)，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
又过(2，－3)
5分
，即
6分
所以
即
①
，其函数开口向上，由题意知①式恒成立， 8分
解之得
又
11分
的取值范围为
12分
