已知在数列{an}中,Sn是数列{an}的前n项和,a1=1且4Sn=an•an+1+1.
(1)求数列{an}的通项公式;
(2)令bn=an•3n-1,数列{bn}的前n项和为Tn.
【答案】
分析:(1)将已知的和与项的递推关系中的n用n-1代替,仿写出一个新的等式,两个式子相减,利用等差数列的定义得到一个等差数列,利用等差数列的通项公式求出通项.
(2)由于数列的通项是一个等差数列与一个等比数列的乘积构成的新数列,利用错位相减法求出数列的前n项和.
解答:解:(1)∵4S
n=a
n•a
n+1+1 ①
∴4S
n-1=a
n-1a
n+1②
②-①得4a
n=a
n(a
n+1-a
n-1)
∵a
n≠0
∴a
n+1-a
n-1=4
∵a
1=1得a
2=3
∴奇数项成以4为公差的等差数列;偶数项成以4为公差的等差数列
∴
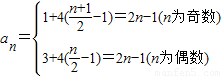
∴a
n=2n-1
(2)∴b
n=(2n-1)•3
n-1∴T
n=1×3
+3×3
1+5×3
2+..+(2n-1)×3
n-13T
n=1×3+3×3
2+5×3
3+…+(2n-3)×3
n-1+(2n-1)×3
n ∴-2T
n=1×3
+2×3+2×3
2+…+2×3
n-1-(2n-1)×3
n ∴
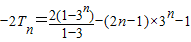
所以T
n=(n-1)3
n+1
点评:已知数列的项与和的递推关系求数列的通项时,一般通过仿写构造一个新等式,两个式子相减得到项的递推关系,再据递推关系的特点选择合适的求通项方法;求数列的前n项和,关键是根据数列通项的特点选择合适的求和方法.

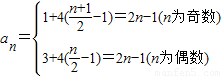
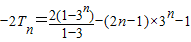


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案