Question

已知函数f(x)=ax²-c,-4≤f(1)≤-1,-1≤f(2)≤5.求f(3)的取值范围.

Answer 1

思路分析:利用f(1)与f(2)设法表示出a,c,然后再代入f(3)的表达式中,从而用f(1)与f(2)来表示f(3),最后运用已知条件确定f(3)的取值范围.也可用线性规划求解.

解:∵f(x)=ax²-c,?

∴即

解得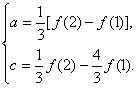

∴f(3)=9a-c=f(2)-f(1).?

又∵-4≤f(1)≤-1,-1≤f(2)≤5,?

∴≤-f(1)≤,　　　　　　　　①

-≤f(2)≤.                               ②

把①②式的两边分别相加得?

-1≤f(2)- f(1)≤20,?

即-1≤f(3)≤20.

温馨提示

在利用不等式基本性质求范围时,一定要强调不等式性质中条件的作用,不等式的两边同乘以(或除以)一个含有字母的式子,一定要知道它的值是正还是负,并且不能为零,才能得到正确的结论.同向不等式只能相加,不能相减.