
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 由题意画出图形,分别求出区域Ω1,Ω2的面积,利用几何概型得答案.
解答 解:如图所示,△OAB对应的区域为Ω1,△OBC对应的区域为Ω2,
联立$\left\{\begin{array}{l}{y=2x}\\{y=3-x}\end{array}\right.$,解得C(1,2),
∴${S}_{△OBC}=\frac{1}{2}×3×1=\frac{3}{2}$,${S}_{△OAB}=\frac{1}{2}×3×3=\frac{9}{2}$,
由几何概型可知,该点落在区域Ω2的概率$P=\frac{{{S_{△OBC}}}}{{{S_{△OAB}}}}=\frac{1}{3}$,
故选B.
点评 本题考查简单的线性规划,考查了几何概型的求法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {3,6} | B. | {4,5} | C. | {2,4,5} | D. | {2,4,5,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-2)∪(1,2) | C. | (-∞,-1)∪(-1,1)∪(3,+∞) | D. | (-∞,-1)∪(-1,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
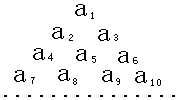 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com