
2![]()
|
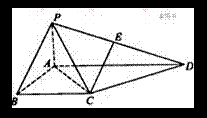 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形, ∠ABC=∠BAD=90°,![]() .
.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE//平面PAB?
若存在,请确定E点的位置;若不存在,请说明理由.
科目:高中数学 来源: 题型:
已知![]()
(1)求![]() 的最大值,及当取最大值时x的取值集合;
的最大值,及当取最大值时x的取值集合;
(2)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意![]() ,且b=1,c=2,求a的值.
,且b=1,c=2,求a的值.
查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修5 3.3 一元二次不等式及其解法练习卷(解析版) 题型:选择题
不等式(x+2)(1-x)>0的解集是( )
A.{x|x<-2或x>1} B.{x|x<-1或x>2}
C.{x|-2<x<1} D.{x|-1<x<2}
查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修一2.3函数应用(I)练习卷(解析版) 题型:解答题
商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年宁夏高三第三次月考文科数学试卷 题型:解答题
选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2。
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,切点为C,若PC=2 ,求PD的长。
,求PD的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com