练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，棱锥的底ABCD是一个矩形，AC与BD交于M，VM是棱锥的高，侧棱都相等且VM⊥AC，VM⊥BD，若VM=4cm，AB=4cm，VC=5cm，求棱锥的全面积及体积．

    答案：略
    解析：

    在中，

    ∴AC=6cm

    ∴

    在等腰三角形VAB中，∵VA=VB=VC=5cm，

    AB=4cm

    所以△VAB底边AB上的高为3cm

    同理△VBC边上的高为

    ∴

    ．

    即棱锥的全面积为，体积为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，△ABC为边长为2的正三角形，点P在A1B上，且AB⊥CP．
    （1）证明：P为A1B中点；
    （2）若A1B⊥AC1，求三棱锥P-A1AC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

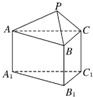    8、如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成，现用3种不同颜色对这个几何体的表面染色（底面A1B1C1不涂色），要求相邻的面均不同色，则不同的染色方案共有
    12
    种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

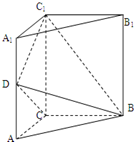    （2014•江门模拟）如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，AC⊥BC，D是棱AA1的中点，AA1=2AC=2BC=2a（a＞0）．
    （1）证明：C1D⊥平面BDC；
    （2）求三棱锥C-BC1D的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

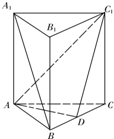    （2012•通州区一模）如图，三棱柱ABC-A1B1C1中，底面为正三角形，AA1⊥平面ABC，且AA1=AB=3，D 是BC的中点．
    （I）求证：A1B∥平面ADC1；
    （II）求证：平面ADC1⊥平面DCC1；
    （III）在侧棱CC1上是否存在一点E，使得三棱锥C-ADE的体积是
    98
    ，若存在，求CE长；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

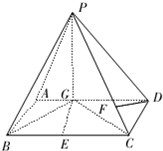    已知如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABC，垂足G在AD上，且AG=
    1
    3
    GD，GB⊥GC．GB=GC=2，PG=4    ，E是BC的中点．
    （1）求证：PC⊥BG；
    （2）求异面直线GE与PC所成角的余弦值；
    （3）若F是PC上一点，且DF⊥GC，求
    CF
    CP
    的值．

    查看答案和解析>>

    同步练习册答案