练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点，（1）若以AB为直径的圆过坐标原点，求实数a的值；（2）是否存在这样的实数a,使A、B两点关于直线y=x对称？若存在，求出a的值;若不存在，请说明理由.

    思路解析：（1）转化为OA⊥OB，即斜率之积为-1；（2）不妨假设存在，然后求值即可.

    解：（1）由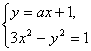消去y,得(3-a2)x2-2ax-2=0.               (1)

    依题意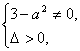即-＜a＜且a≠±.                        (2)

    设A(x1,y1)，B(x2,y2),则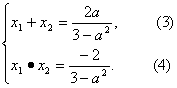

    ∵以AB为直径的圆过原点，∴OA⊥OB.∴x1x2+y1y2=0.

    但y1·y2=a2x1x2+a(x1+x2)+1,

    由(3)(4),得x1+x2=,x1x2=,

    ∴(a2+1)·+a·+1=0.解得a=±1且满足(2).

    （2）假设存在实数a，使A、B关于y=x对称，则直线y=ax+1与y=x垂直，∴a=-2.直线l的方程为y=-2x+1.

    将a=-2代入(3),得x1+x2=4,∴AB中点横坐标为2，

    纵坐标为y=-2×2+1=-3.但AB中点（2，-3）不在直线y=x上，即不存在实数a使A、B关于直线y=x对称.

    方法归纳

        （1）直线与双曲线的关系问题，往往采用“设而不求”的方法，结合韦达定理求解；（2）开放性问题，则经常采用假设存在，直接推证的方法.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知直线y=ax+1与双曲线3x2-y2=1；
    （1）当a为何值时，直线与双曲线有一个交点；
    （2）直线与双曲线交于P、Q两点且以PQ为直径的圆过坐标原点，求a值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点，
    （1）若以AB线段为直径的圆过坐标原点，求实数a的值．
    （2）是否存在这样的实数a，使A、B两点关于直线y=
    12
    x    对称？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线y=ax+1与双曲线3x2-y2=1相交于A、B两点，若以AB为直径的圆经过坐标原点，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点，（1）若以AB线段为直径的圆过坐标原点，求实数a的值。（2）是否存在这样的实数a，使A、B两点关于直线对称？说明理由。

    查看答案和解析>>

    科目：高中数学 来源：2013届甘肃省高二第一学期期末考试数学试卷 题型：解答题

    已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点。

    （1）若以AB线段为直径的圆过坐标原点，求实数a的值。

    （2）是否存在这样的实数a，使A、B两点关于直线对称？说明理由。

     

    查看答案和解析>>

    同步练习册答案