
(1)作函数 的图像,并说明该图像与
的图像,并说明该图像与 的图像的关系;
的图像的关系;
(2)作函数 的图像,并说明该图像与
的图像,并说明该图像与 的图像的关系.
的图像的关系.
|
先将函数的解析式化简为我们熟悉的函数的解析式. 解: (1)
从而得到函数图像的画法如下: ①作  的图像,如图(1)所示. 的图像,如图(1)所示.
②以 x轴为对称轴作已作抛物线在-4<x<1部分的对称图形,则 在x≥1,x≤-4的图形及其在-4<x<1部分的关于x轴的对称图像便为所求(如图(2)所示). 在x≥1,x≤-4的图形及其在-4<x<1部分的关于x轴的对称图像便为所求(如图(2)所示).
该函数图像与  图像的关系是:将 图像的关系是:将 在x轴下方部分翻折到x轴上方而得到. 在x轴下方部分翻折到x轴上方而得到.
② 
图像如图所示.
该图像与  的图像的关系是:将 的图像的关系是:将 的y轴的左方部分去掉,作y轴右方部分关于y轴的对称图像而得到. 的y轴的左方部分去掉,作y轴右方部分关于y轴的对称图像而得到. |
|
(1)y=f(x)与y=|f(x)|的图像之间的关系是将y=f(x)在x轴下方的部分翻折到x轴上方而得到y=|f(x)|的图像(下方部分不再保留) (2)y=f(x)与y=f(|x|)的图像之间的关系是:将y=f(x)在y轴左方部分去掉,作右方部分关于y轴的对称图像,从而形成一个关于y轴对称的函数图像,便得y=f(|x|)的图像. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010-2011学年湖北省高三上学期期末考试数学文卷 题型:解答题
(本小题满分13分)
已知点 是函数
是函数 的图像上的两点,若对于任意实数
的图像上的两点,若对于任意实数 ,当
,当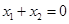 时,以
时,以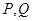 为切点分别作函数
为切点分别作函数 的图像的切线,则两切线必平行,并且当
的图像的切线,则两切线必平行,并且当 时函数
时函数 取得极小值1.[来源:]
取得极小值1.[来源:]
(1)求函数 的解析式;
的解析式;
(2)若 是函数
是函数 的图像上的一点,过
的图像上的一点,过 作函数
作函数 图像的切线,切线与
图像的切线,切线与 轴和直线
轴和直线 分别交于
分别交于 两点,直线
两点,直线 与
与 轴交于
轴交于 点,求△ABC的面积的最大值.
点,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2010年河北省高三押题数学(理)试题 题型:选择题
图1是函数 的图像,A(x,y)是图像上任意一点,过点A作x轴的平行线,交其图像于另一点B(A,B可重合)。设线段AB的长为f(x),则函数f(x)的图像是 ( )
的图像,A(x,y)是图像上任意一点,过点A作x轴的平行线,交其图像于另一点B(A,B可重合)。设线段AB的长为f(x),则函数f(x)的图像是 ( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com