解:(1)由4cosC

,
化简得:4cosC•

+2cos
2C-1=0,
即cosC=

,又C为三角形的内角,则有C=

,
∴sinC=

,又C=π-(A+B),
∴sin(A+B)=

,
∵tanA=2tanB,
∴

=

=

=3,
则sin(A-B)=

;
(2)根据正弦定理

=

=

=2R,
得到a=2RsinA,b=2RsinB,又sinC=

,
则△ABC面积S=

absinC
=

R
2sinAsinB
=

R
2sinAsin(

-A)
=

R
2(

sinAcosA+

sin
2A)
=

R
2[

sin(2A-

)+

],
当2A-

=

,即A=

时,
正弦函数sin(2A-

)取得最大值1,此时面积S取得最大值为

R
2,
此时三角形为等边三角形,则有a=b=c,
∴3ab=25-c
2化简得:c=

,
此时R=

=
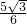
,
则三角形ABC面积的最大值为

=
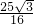
.
分析:(1)把已知的等式左边第一项的第二个因式利用二倍角的余弦函数公式化简,第二项也利用二倍角的余弦函数公式化简,约分去括号合并后,求出cosC的值,由C为三角形的内角利用特殊角的三角函数值得到C的度数,进而求出sinC的值,进而由三角形的内角和定理及诱导公式得到sin(A+B)的值,然后利用两角和与差的正弦函数公式化简

后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanA=2tanB代入求出

的值,把sin(A+B)的值代入即可求出sin(A-B)的值;
(2)根据正弦定理

=

=

=2R,表示出a与b,再由sinC的值,利用三角形的面积公式S=

absinA表示出三角形ABC的面积,根据C的度数,求出A+B的度数,用A表示出B,代入表示出的面积中,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,整理后再利用二倍角的正弦、余弦函数公式化简,最后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域表示出面积S的最大值,并求出此时A的度数,得到三角形ABC为等边三角形,即a=b=c,代入已知的等式3ab=25-c
2,求出c的值,再由sinC的值,求出三角形外接圆半径R,代入表示出的S最大值的式子中即可求出三角形ABC面积的最大值.
点评:此题属于解三角形的题型,涉及的知识有:二倍角的正弦、余弦函数公式,诱导公式,两角和与差的正弦函数公式,正弦函数的定义域和值域,等边三角形的性质,以及正弦定理,本题的技巧性较强,熟练掌握公式及定理是解本题的关键.

 .
. ,
, +2cos2C-1=0,
+2cos2C-1=0, ,又C为三角形的内角,则有C=
,又C为三角形的内角,则有C= ,
, ,又C=π-(A+B),
,又C=π-(A+B), ,
, =
= =
= =3,
=3, ;
; =
= =
= =2R,
=2R, ,
, absinC
absinC R2sinAsinB
R2sinAsinB R2sinAsin(
R2sinAsin( -A)
-A) R2(
R2( sinAcosA+
sinAcosA+ sin2A)
sin2A) R2[
R2[ sin(2A-
sin(2A- )+
)+ ],
], =
= ,即A=
,即A= 时,
时, )取得最大值1,此时面积S取得最大值为
)取得最大值1,此时面积S取得最大值为 R2,
R2, ,
, =
=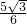 ,
, =
=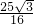 .
. 后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanA=2tanB代入求出
后,分子分母同时除以cosαcosβ,利用同角三角函数间的基本关系弦化切后,将tanA=2tanB代入求出 的值,把sin(A+B)的值代入即可求出sin(A-B)的值;
的值,把sin(A+B)的值代入即可求出sin(A-B)的值; =
= =
= =2R,表示出a与b,再由sinC的值,利用三角形的面积公式S=
=2R,表示出a与b,再由sinC的值,利用三角形的面积公式S= absinA表示出三角形ABC的面积,根据C的度数,求出A+B的度数,用A表示出B,代入表示出的面积中,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,整理后再利用二倍角的正弦、余弦函数公式化简,最后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域表示出面积S的最大值,并求出此时A的度数,得到三角形ABC为等边三角形,即a=b=c,代入已知的等式3ab=25-c2,求出c的值,再由sinC的值,求出三角形外接圆半径R,代入表示出的S最大值的式子中即可求出三角形ABC面积的最大值.
absinA表示出三角形ABC的面积,根据C的度数,求出A+B的度数,用A表示出B,代入表示出的面积中,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,整理后再利用二倍角的正弦、余弦函数公式化简,最后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,根据正弦函数的值域表示出面积S的最大值,并求出此时A的度数,得到三角形ABC为等边三角形,即a=b=c,代入已知的等式3ab=25-c2,求出c的值,再由sinC的值,求出三角形外接圆半径R,代入表示出的S最大值的式子中即可求出三角形ABC面积的最大值.

 阅读快车系列答案
阅读快车系列答案