
证明:(Ⅰ)取AC中点D,连接SO.
∵SO⊥面ABC,
∴AC⊥SO,
∵△ABC是边长为4的正三角形,
∴AC⊥BO
∴AC⊥面SOB,∴AC⊥SB.
(Ⅱ)过N作ND∥SO交OB于D,则ND⊥面ABC,且D是OB的中点,
在Rt△NCD中,ND=

SO=

CD=

∴CN=3
∴cos∠NCD=

.
直线CN与平面ABC所成角的余弦值

.
(Ⅲ)解:在Rt△SDE中,SE=

,CM是边长为4正△ABC的中线,

.
∴S
△SCM=

CM•SE=

,
设点B到平面SCM的距离为h,
由V
B-SCM=V
S-CMB,SD⊥平面ABC,得

S
△SCM•h=

S
△CMB•SD,
∴h=

.即点B到平面SCM的距离为
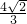
.
分析:(1)欲证AC⊥SB,取AC中点D,连接DS、DB.根据线面垂直的性质定理可知,只须证AC⊥SD且AC⊥DB,即得;
(2)欲求直线CN与平面ABC所成角的余弦值大小,可先作出直线CN与平面ABC所成角,结合SD⊥平面ABC.过D作DE⊥CM于E,连接SE,则SE⊥CM,从而得出∠NCD为直线CN与平面ABC所成角.最后在Rt△NCD中求解即可;
(3)设点B到平面CMN的距离为h,利用等到体积法:V
B-SNM=V
S-NMB,即可求得点B到平面CMN的距离.
点评:本小题主要考查直线与直线,直线与平面所成角,点到平面的距离等基础知识,考查空间想象能力和逻辑推理能力.求距离的关键是构造三棱锥的体积求解.

 在三棱锥S-ABC中,△ABC是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,SA=
在三棱锥S-ABC中,△ABC是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,SA= ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点. 证明:(Ⅰ)取AC中点D,连接SO.
证明:(Ⅰ)取AC中点D,连接SO. SO=
SO=
 ∴CN=3
∴CN=3 .
. .
. ,CM是边长为4正△ABC的中线,
,CM是边长为4正△ABC的中线, .
. CM•SE=
CM•SE= ,
, S△SCM•h=
S△SCM•h= S△CMB•SD,
S△CMB•SD, .即点B到平面SCM的距离为
.即点B到平面SCM的距离为 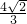 .
.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.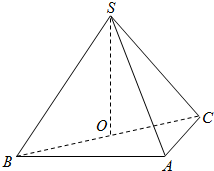 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2 C.
C. 如图,在三棱锥S-ABC中,SA=AB=BC=AC=
如图,在三棱锥S-ABC中,SA=AB=BC=AC=