若函数f(x)=x2+(a+2)x+3,x∈[a,b],且满足f(x-1)=f(1+x),则a=________,b=________.
-4 6
分析:由已知等式f(1-x)=f(1+x),根据函数图象的对称性,我们可得函数f(x)的图象关于直线 x=1对称,由此可求出a值,再由函数恒满足等式f(1-x)=f(1+x),
则区间[a,b]也关于直线 x=1对称对称,由此求出b的值,即可得到答案.
解答:∵函数f(x)满足f(x+1)=f(x-1),故有 f(x+2)=f(x),
故函数f(x)的图象关于直线 x=1对称,又∵函数f(x)=x
2+(a+2)x+3,
∴-
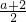
=1,∴a=-4.
又∵x∈[a,b],故区间[a,b]也关于直线 x=1对称,由此求得b=6,
故答案为:-4,6.
点评:本题考查的知识点是二次函数的图象和性质,函数图象的对称性,其中根据已知中函数f(x)恒满足等式f(1-x)=f(1+x),得到函数f(x)的图象关于直线 x=1对称,是解答本题的关键,另外根据函数的解析式以及函数图象关于直线 x=1对称对称,是进一步求出b值的关键,属于基础题.

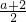 =1,∴a=-4.
=1,∴a=-4.
