Question

已知数列{a_n},{b_n}是各项均为正数的等比数列,设c_n=(n∈N^*).

(1)数列{c_n}是否为等比数列?证明你的结论.

(2)设数列{lna_n},{lnb_n}的前n项和分别为S_n,T_n.若a₁=2,,求数列{c_n}的前n项和.

Answer 1

答案：本题主要考查等差数列、等比数列、对数等基础知识,考查综合运用数学知识解决问题的能力.

解:(1){c_n}是等比数列,                                                        

证明:设{a_n}的公比为q₁(q₁＞0),{b_n}的公比为q₂(q₂＞0),则

,故{c_n}为等比数列.                      

(2)数列{lna_n}和{lnb_n}分别是公差为lnq₁和lnq₂的等差数列.

由条件得,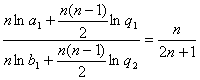

即                                              

故对n=1,2,…,

(2lnq₁-lnq₂)n²+(4lna₁-lnq₁-2lnb₁+lnq₂)n+(2lna₁-lnq₁)=0.

于是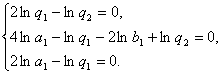

将a₁=2代入得q₁=4,q₂=16,b₁=8.                                              

从而有c_n==4ⁿ.

所以数列{c_n}的前n项和为4+4²+…+4ⁿ=(4ⁿ-1).