练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    从南到北的铁路干线经过甲城与乙城，两城之间的距离为15 km，某工厂位于乙城正西2 km处.现要从甲城把货物运往工厂，在铁路线上的运费每千米3元，而沿公路上的运费每千米5元，为了使货物从甲城运到工厂的运费最省，应该从铁路干线上的何处起修筑通到工厂的公路较为恰当？

    解：设在距乙城x( km)处的点C修筑公路运费最省，总费用为y，则有y=3(15-x)+5 (0≤x≤15),所以y′=-3+,由y′=0得5x=3,即x=,所以y的最小值只可能在x=处取得.因为f()=53.所以当x=时，y最小.即在离乙城1.5 km处修筑通到工厂的公路较恰当.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网已知函数f(x)=
    x2
    x+m
    的图象经过点（4，8）．
    （1）求该函数的解析式；
    （2）数列{an}中，若a1=1，Sn为数列{an}的前n项和，且满足an=f（Sn）（n≥2），
    证明数列{
    1
    Sn
    }    成等差数列，并求数列{an}的通项公式；
    （3）另有一新数列{bn}，若将数列{bn}中的所有项按每一行比上一行多一项的规则排成如下数表：记表中的第一列数b1，b2，b4，b7，…，构成的数列即为数列{an}，上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列，且公比为同一个正数．当b81=-
    4
    91
    时，求上表中第k（k≥3）行所有项的和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    甲同学家到乙同学家的途中有一公园，甲从家到公园的距离与乙从家到公园的距离都是2km，甲10 时出发前往乙家．如图：所示，表示甲从家出发到乙家为止经过的路程y（km）与时间x（分）的关系．试写出y=f（x）的函数解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在下列五个命题中：
    ①若a=3
    		2
    ，则a⊆{x}x＞2
    		3
    }；
    ②若P={x|0≤x≤4}，Q={ y|0≤y≤2}，则对应y=
    3x
    2
    不是从P到Q的映射；
    ③f(x)=
    3
    x
    在（-∞，0）∪（0，+∞）上为减函数；
    ④若函数y=f（x-1）的图象经过点（4，1），则函数y=f-1（x）的图象必经过点（1，3）；
    ⑤命题“对任意的x∈R，x3-x2+1≤0”的否定是“不存在x∈R，x3-x2+1≤0”．
    其中所有不正确的命题的序号为
    ①③⑤
    ①③⑤
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

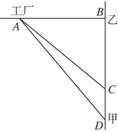
    如图，铁路线上AC段长99km，工厂B到铁路的距离BC为20km，现在要在AC上某一点D处，向B修一条公路，已知铁路每吨千米与公路每吨千米的运费之比为λ（0＜λ＜1），为了使从A到B的运费最省，D应选在离C距离多远处．

    查看答案和解析>>

    同步练习册答案