
科目:高中数学 来源:2014届浙江省杭州市高二5月月考理科数学试卷(解析版) 题型:填空题
对于三次函数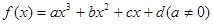 ,定义
,定义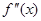 是
是 的导函数
的导函数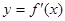 的导函数,若方程
的导函数,若方程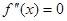 有实数解
有实数解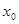 ,则称点
,则称点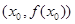 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数都关于点 对称:
对称:
②存在三次函数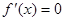 有实数解
有实数解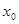 ,点
,点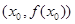 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则:
,则: 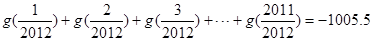
其中正确命题的序号为__ __(把所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义f″(x)是y=f(x)的导函数y=f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有的同学发现“任何三次函数都有‘拐点’;任何三次函数都有对称中心;且对称中心就是‘拐点’”.请你根据这一发现判断下列命题:
(1)任意三次函数都关于点![]() 对称;
对称;
(2)存在三次函数,f'(x)=0有实数解x0,(x0,f(x0))点为函数y=f(x)的对称中心;
(3)存在三次函数有两个及两个以上的对称中心;
(4)若函数![]() ,则
,则![]()
其中正确命题的序号为( )
|
| A. | (1)(2)(4) | B. | (1)(2)(3)(4) | C. | (1)(2)(3) | D. | (2)(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com