练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,中，，若为的外心，则             .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．
    （1）证明：BD⊥平面PAC；
    （2）若AD=2，当PC与平面ABCD所成角的正切值为
    		2
    2
    时，求四棱锥P-ABCD的外接球表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某同学向如图所示的圆形靶投掷飞镖，飞镖落在靶外（环数记为0）的概率为0.1，飞镖落在靶内的各个点是随机的．已知圆形靶中三个圆为同心圆，半径分别为30cm、20cm、10cm，飞镖落在不同区域的环数如图中标示．
    （1）若这位同学向圆形靶投掷3次飞镖，求恰有2次落在9环区域内的概率；
    （2）记这位同学投掷一次得到的环数为随机变量X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

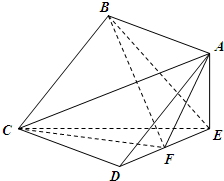    （2012•黄山模拟）如图，在四棱锥E-ABCD中，底面ABCD为正方形，AE⊥平面CDE，已知AE=3，DE=4．
    （Ⅰ）若F为DE的中点，求证：BE∥平面ACF；
    （Ⅱ）求直线BE与平面ABCD所成角的正弦值；
    （Ⅲ）如果四棱锥E-ABCD有外接球，求出四棱锥E-ABCD外接球的半径，没有的话请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

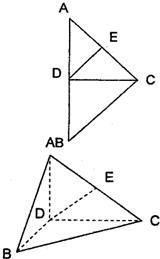    精英家教网如图，在Rt△ABC中，∠ACB=90°，AC=BC=4，D是AB中点，E是AC的中点，现将△ABC沿CD翻折成直二面角A-DC-B．
    （1）求异面直线AB与DE所成的角；
    （2）若M，N分别为棱AC，BC上的动点，求△DMN周长的平方的最小值；
    （3）在三棱锥D-ABC的外接球面上，求A，B两点间的球面距离和外接球体积．

    查看答案和解析>>

    科目：高中数学 来源：2014届安徽省高一下学期期中考试数学试卷（解析版） 题型：解答题

    如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、

    PC的中点．

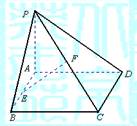
    （1）求证：EF∥平面PAD；

    （2）求证：EF⊥CD；

    （3）若ÐPDA＝45°求EF与平面ABCD所成的角的大小．

    【解析】本试题主要考查了线面平行和线线垂直的运用，以及线面角的求解的综合运用

    第一问中，利用连AC，设AC中点为O，连OF、OE在△PAC中，∵ F、O分别为PC、AC的中点   ∴ FO∥PA …………①在△ABC中，∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又         ∵ BC∥AD   ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD∵ EF Ì 平面EFO   ∴ EF∥平面PAD．

    第二问中在矩形ABCD中，∵ EO∥BC，BC⊥CD ∴ EO⊥CD  又    ∵ FO∥PA，PA⊥平面AC  ∴ FO⊥平面AC∴ EO为EF在平面AC内的射影       ∴ CD⊥EF．

    第三问中，若ÐPDA＝45°，则 PA＝AD＝BC    ∵ EOBC，FOPA

    ∴ FO＝EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO＝45°

    证：连AC，设AC中点为O，连OF、OE（1）在△PAC中，∵ F、O分别为PC、AC的中点∴ FO∥PA …………①    在△ABC中，∵ E、O分别为AB、AC的中点  ∴ EO∥BC ,又         ∵ BC∥AD   ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD    

    ∵ EF Ì 平面EFO      ∴ EF∥平面PAD．

    （2）在矩形ABCD中，∵ EO∥BC，BC⊥CD∴ EO⊥CD  又        ∵ FO∥PA，PA⊥平面AC  ∴ FO⊥平面AC ∴ EO为EF在平面AC内的射影     ∴ CD⊥EF．

    （3）若ÐPDA＝45°，则 PA＝AD＝BC         ∵ EOBC，FOPA

    ∴ FO＝EO 又    ∵ FO⊥平面AC   ∴ △FOE是直角三角形 ∴ ÐFEO＝45°

     

    查看答案和解析>>

    同步练习册答案