练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    研究方程e－x＝log2x根的个数．

    答案：
    解析：

    　　我们可以令f(x)＝e－x，g(x)＝log2x，可知方程f(x)＝g(x)的实根个数即函数y＝f(x)的图象与y＝g(x)的图象的公共点个数．此两种函数均为基本初等函数，图象可以容易地做出．如图．

    　　由图可知，两函数图象一增一减，有且只有一个公共点，也就是说原方程有且只有一个实数解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：重庆市西南师大附中2010届高三下学期3月月考数学文科试题 题型：013

    已知函数f(x)＝|log2|x－1||，且关于x的方程[f(x)]2＋af(x)＋b＝0有6个不同的实数解，若最小实数解为–3，则a＋b的值为

    [　　]
    A．

    －3

    B．

    －2

    C．

    0

    D．

    不能确定

    查看答案和解析>>

    科目：高中数学 来源：重庆市重庆八中2011届高三第七次月考数学文科试题 题型：022

    记f(x)＝log2(x－1)的反函数为y＝f－1(x)，则方程f－1(x)＝9的解x＝________．

    查看答案和解析>>

    科目：高中数学 来源：2008年普通高等学校招生全国统一考试(上海卷)、数学 题型：044

    已知函数f(x)＝log2(2x＋1)．

    (1)求证：函数f(x)在(－∞，＋∞)内单调递增；

    (2)记f－1(x)为函数f(x)的反函数．若关于x的方程f－1(x)＝m＋f(x)在[1，2]上有解，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年河北省高三8月月考理科数学试卷（解析版） 题型：解答题

    已知函数　f(x)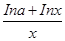＝在[1，＋∞)上为减函数，求实数a的取值范围.

    【解析】本试题考查了导数在研究函数中的运用。根据函数f(x)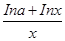＝在[1，＋∞)上为减函数，可知导函数在给定区间恒小于等于零，f ′(x)≤0在[1，＋∞)上恒成立，lna≥1－lnx在[1，＋∞)上恒成立．然后利用φ(x)＝1－lnx，φ(x)max＝1，从而得到a≥e

    f ′(x)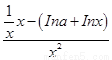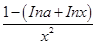＝＝，因为　f(x)在[1，＋∞)上为减函数，故　f ′(x)≤0在[1，＋∞)上恒成立，即lna≥1－lnx在[1，＋∞)上恒成立．设φ(x)＝1－lnx，φ(x)max＝1，故lna≥1，a≥e，

     

    查看答案和解析>>

    同步练习册答案