练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)＝2＋log3x(1≤x≤9)，求函数g(x)＝[f(x)]2＋f(x2)的最大值与最小值．

    答案：
    解析：

    　　分析：将函数f(x)的解析式代入g(x)，得到g(x)的解析式，再以log3x为未知数进行配方，但需注意先根据函数f(x)的定义域确定log3x的取值范围．

    　　解：由f(x)的定义域为[1，9]知，

    　　在函数g(x)中满足解得1≤x≤3，

    　　所以0≤log3x≤1．

    　　又g(x)＝(2＋log3x)2＋(2＋log3x2)＝(log3x＋3)2－3，0≤log3x≤1，

    　　令t＝log3x，则g(t)＝(t＋3)2－3，t∈[0，1]，

    　　显然，g(t)在[0，1]上单调递增，

    　　因为g(0)＝6，g(1)＝13，

    　　所以，当t＝0，即x＝1时，g(x)有最小值6；

    　　当t＝1，即x＝3时，g(x)有最大值13．

    　　点评：求函数最值的前提是正确确定函数的定义域．解本题的关键是由x的取值范围确定log3x的取值范围．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：湖南省长沙市一中2010届高三上学期第二次月考(数学理) 题型：022

    已知函数f(x)＝，直线l：9x＋2y＋c＝0，当x∈[－2，2]时，函数y＝f(x)图象恒在直线l的下方，则c的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源：重庆市重庆一中2012届高三9月月考数学理科试题 题型：044

    若存在实数k和b，使得函数f(x)与g(x)对其定义域上的任意实数x分别满足：f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为f(x)与g(x)的“和谐直线”．已知h(x)＝x2，(x)＝2elnx，(e为自然对数的底数)；

    (1)求F(x)＝h(x)－(x)的极值；

    (2)函数h(x)和(x)是否存在和谐直线？若存在，求出此和谐直线方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012年陕西省高二下期第一次月考理科数学试卷（解析版） 题型：解答题

    已知函数f(x)＝x3－3x及y＝f(x)上一点P(1，－2)，过点P作直线l.

    (1)求使直线l和y＝f(x)相切且以P为切点的直线方程；

    (2)求使直线l和y＝f(x)相切且切点异于P的直线方程．

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学导数专项训练（河北） 题型：解答题

    已知函数f(x)＝x3－2x2＋ax(x∈R，a∈R)，在曲线y＝f(x)的所有切线中，有且仅有一条切线l与直线y＝x垂直．

    (1)求a的值和切线l的方程；

    (2)设曲线y＝f(x)上任一点处的切线的倾斜角为θ，求θ的取值范围

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年甘肃省天水市高三第六次检测数学文卷 题型：解答题

    （12分）已知动点P到定点F (, 0 ) 的距离与点 P 到定直线 l：x＝2 的距离之比为。

    （1）求动点P的轨迹C的方程；

    （2）设M、N是直线l上的两个点，点E是点F关于原点的对称点，若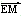·＝0，

        求 | MN | 的最小值。

     

    查看答案和解析>>

    同步练习册答案