练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若α＋β＝45°，则(1＋tanα)(1＋tanβ)＝________．

    答案：2
    解析：

    　　将所求式子展开变形用两角和的正切即可．

    　　原式＝1＋tanα＋tanβ＋tanαtanβ

    　　＝1＋tan(α＋β)(1－tanαtanβ)＋tanαtanβ

    　　＝1＋tan45°(1－tanαtanβ)＋tanαtanβ

    　　＝1＋1－tanαtanβ＋tanαtanβ＝2．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(必修5)　2009－2010学年　第5期　总第161期 北师大课标版(必修5) 题型：013

    在△ABC中，若a＝12，b＝24，A＝45°，则此三角形解的情况为

    [　　]
    A．

    无解

    B．

    两解

    C．

    一解

    D．

    解的个数不能确定

    查看答案和解析>>

    科目：高中数学 来源：辽宁省东北育才学校高中部2008－2009学年高一下学期第一次月考数学试题 题型：022

    在△ABC中，角A，B，C的对边为a，b，c，若，，B＝45°，则角C＝________．

    查看答案和解析>>

    科目：高中数学 来源：河南省郑州外国语学校2012届高三下学期综合测试验收(5)数学理科试题 题型：013

    过双曲线(a＞0，b＞0)的左焦点F1作x轴的垂线交双曲线于点P，F2为右焦点，若∠F1PF2＝45°，则双曲线的离心率为

    [　　]

    A．

    B．

    C．

    D．2

    查看答案和解析>>

    科目：高中数学 来源：2014届浙江效实中学高二上期末考试理科数学试卷（解析版） 题型：选择题

    如图所示，已知椭圆的方程为 ，A为椭圆的左顶点，B，C在椭圆上，若四边形OABC为平行四边形，且∠OAB＝45°，则椭圆的离心率等于（   ）

    A．            B．             C．             D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届安徽省高一下学期期中考试数学试卷（解析版） 题型：解答题

    如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、

    PC的中点．

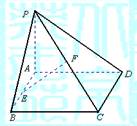
    （1）求证：EF∥平面PAD；

    （2）求证：EF⊥CD；

    （3）若ÐPDA＝45°求EF与平面ABCD所成的角的大小．

    【解析】本试题主要考查了线面平行和线线垂直的运用，以及线面角的求解的综合运用

    第一问中，利用连AC，设AC中点为O，连OF、OE在△PAC中，∵ F、O分别为PC、AC的中点   ∴ FO∥PA …………①在△ABC中，∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又         ∵ BC∥AD   ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD∵ EF Ì 平面EFO   ∴ EF∥平面PAD．

    第二问中在矩形ABCD中，∵ EO∥BC，BC⊥CD ∴ EO⊥CD  又    ∵ FO∥PA，PA⊥平面AC  ∴ FO⊥平面AC∴ EO为EF在平面AC内的射影       ∴ CD⊥EF．

    第三问中，若ÐPDA＝45°，则 PA＝AD＝BC    ∵ EOBC，FOPA

    ∴ FO＝EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO＝45°

    证：连AC，设AC中点为O，连OF、OE（1）在△PAC中，∵ F、O分别为PC、AC的中点∴ FO∥PA …………①    在△ABC中，∵ E、O分别为AB、AC的中点  ∴ EO∥BC ,又         ∵ BC∥AD   ∴ EO∥AD …………②综合①、②可知：平面EFO∥平面PAD    

    ∵ EF Ì 平面EFO      ∴ EF∥平面PAD．

    （2）在矩形ABCD中，∵ EO∥BC，BC⊥CD∴ EO⊥CD  又        ∵ FO∥PA，PA⊥平面AC  ∴ FO⊥平面AC ∴ EO为EF在平面AC内的射影     ∴ CD⊥EF．

    （3）若ÐPDA＝45°，则 PA＝AD＝BC         ∵ EOBC，FOPA

    ∴ FO＝EO 又    ∵ FO⊥平面AC   ∴ △FOE是直角三角形 ∴ ÐFEO＝45°

     

    查看答案和解析>>

    同步练习册答案