解答:解:(Ⅰ)函数f(x)的定义域为R,
f′(x)==.
当a>0时,
当x变化时,f'(x),f(x)的变化情况如下表:
| x |
(-∞,-1) |
-1 |
(-1,1) |
1 |
(1,+∞) |
| f'(x) |
- |
0 |
+ |
0 |
- |
| f(x) |
↘ |
|
↗ |
|
↘ |
当a<0时,
当x变化时,f'(x),f(x)的变化情况如下表:
| x |
(-∞,-1) |
-1 |
(-1,1) |
1 |
(1,+∞) |
| f'(x) |
+ |
0 |
- |
0 |
+ |
| f(x) |
↗ |
|
↘ |
|
↗ |
综上所述,
当a>0时,f(x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f(x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
…(5分)
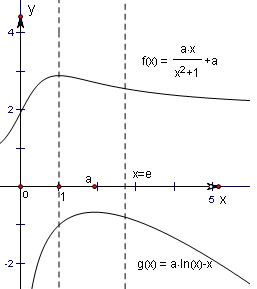
(Ⅱ)由(Ⅰ)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,
又f(0)=a,f(e)=
f(e)=+a>a所以f(x)
min=a,
同样地,当a>0时,g(x)在(0,a)上单调递增,g(x)在(a,e]上单调递减,
所以g(x)
max=g(a)=alna-a,
因为a-(alna-a)=a(2-lna)>a(2-lne)=a>0,
所以对于任意x
1,x
2∈(0,e],总有g(x)
max=g(e)=alna-a<a=f(x)
min.
所以对于任意x
1,x
2∈(0,e],仍有x
1,x
2∈(0,e].
综上所述,对于任意x
1,x
2∈(0,e],总有g(x
1)<f(x
2)成立.…(13分)

 (Ⅱ)由(Ⅰ)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,
(Ⅱ)由(Ⅰ)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,

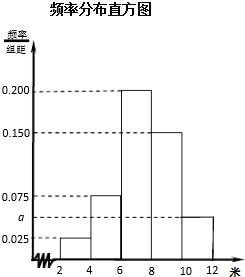 (2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.