
(08年龙岩一中模拟文)(12分)
四棱锥S―ABCD的底面是直角梯形,![]() ,侧面SBC⊥底面ABCD
,侧面SBC⊥底面ABCD
(Ⅰ)由SA的中点E作底面的垂线EH,试确定垂足H的位置;
(Ⅱ)求二面角E―BC―A的大小.
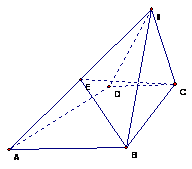
解析:(Ⅰ)作SO⊥BC于O,则SO![]() 平面SBC,
平面SBC,
又面SBC⊥底面ABCD
面SBC∩面ABCD=BC,
∴SO⊥底面ABCD,①
又SO![]() 平面SAO,∴面SAO⊥底面ABCD……4分
平面SAO,∴面SAO⊥底面ABCD……4分
作EH⊥AO,∴EH⊥面ABCD②
即H为垂足,由①、②知,EH//SO,
又E为SA的中点,∴H是AO的中点……………………………………………6分
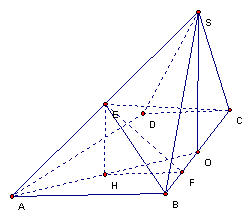
(Ⅱ)过H作HF⊥BC于F,连EF,又(I)知EH⊥平面ABCD,∴EH⊥BC,
∴BC⊥平面EFH,∴BC⊥EF,
∴∠HFE为面EBC和底面ABCD所成二面角的平面角.………………9分
在等边△SBC中,∵SO⊥BC,∴O为BC中点,又BC=2,
![]() ,
,
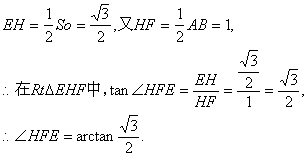
∴二面角E―BC―A为![]() ……………12分
……………12分


科目:高中数学 来源: 题型:
(08年龙岩一中模拟)(12分)
如图,三棱锥P―ABC中, PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB.
平面PAB.
(Ⅰ) 求证:AB![]() 平面PCB;
平面PCB;
(Ⅱ)求异面直线AP与BC所成角的大小;
(Ⅲ)求二面角C-PA-B的大小的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中模拟文)(12分)
设a、b、c分别是先后三次抛掷一枚骰子得到的点数。
(Ⅰ)求a+b+c为奇数的概率
(Ⅱ)设有关于![]() 的一元二次方程
的一元二次方程![]() ,求上述方程有两个不相等实根的概率.
,求上述方程有两个不相等实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中模拟理)(14分)
已知函数![]() ,
,![]() .
.
(1)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(2)对于给定的闭区间![]() ,试说明存在实数
,试说明存在实数 ![]() ,当
,当![]() 时,
时,![]() 在闭区间
在闭区间![]() 上是减函数;
上是减函数;
(3)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中模拟)(12分)
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得![]() 分. 现从盒内一次性取3个球.
分. 现从盒内一次性取3个球.
(Ⅰ)求取出的3个球得分之和恰为1分的概率;
(Ⅱ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com