
数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…, ![]() ,
,![]() ,…,
,…,![]() ,…有如下运算和结论:
,…有如下运算和结论:
①![]() ; ②
; ②![]() ;
;
③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列
,…是等比数列
④数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;
;
⑤若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .
.
在后面横线上填写出所有你认为正确运算结果或结论的序号______________.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源:2010年重庆市高考数学理科适应性考试试题 题型:解答题
(12分) 设数列 的前
的前 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数 的图象上. (1) 求数列
的图象上. (1) 求数列 的通项公式; (2) 将数列
的通项公式; (2) 将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),(
),( ,
, ),(
),( ,
, ,
, ),(
),( ,
, ,
, ,
, );(
);( ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求 的值;(3)设
的值;(3)设 为数列
为数列 的前
的前 项积,若不等式
项积,若不等式 对一切
对一切 都成立,求
都成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省、鹰潭一中高三4月联考理科数学试卷(解析版) 题型:解答题
设数列 的前
的前 项和为
项和为 ,且满足
,且满足
(1)求数列 的通项公式;
的通项公式;
(2)在数列 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列 ,在
,在 两项之间插入
两项之间插入 个数,使这
个数,使这 个数构成等差数列,求
个数构成等差数列,求 的值;
的值;
(3)对于(2)中的数列 ,若
,若 ,并求
,并求 (用
(用 表示).
表示).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市徐汇区高三第一学期学习能力诊断卷理科数学 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,
第3小题满分6分.
设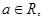 把三阶行列式
把三阶行列式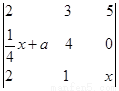 中第一行第二列元素的余子式记为
中第一行第二列元素的余子式记为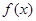 ,且关于
,且关于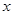 的不等式
的不等式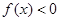 的解集为
的解集为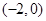 。各项均为正数的数列
。各项均为正数的数列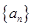 的前
的前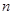 项和为
项和为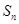 ,点列
,点列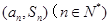 在函数
在函数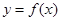 的图象上。
的图象上。
(1)求函数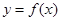 的解析式;
的解析式;
(2)若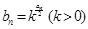 ,求
,求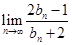 的值;
的值;
(3)令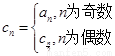 ,求数列
,求数列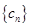 的前
的前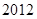 项中满足
项中满足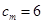 的所有项数之和.
的所有项数之和.
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(上海) 题型:解答题
若有穷数列 (
(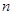 是正整数),满足
是正整数),满足 即
即
( 是正整数,且
是正整数,且 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且 成等差数列,
成等差数列, ,试写出
,试写出 的每一项
的每一项
(2)已知 是项数为
是项数为 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com