练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若x+y≥m时满足x2+y2=1的任意实数对(x,y)都成立，则m的最大值为

    A.0                    B.              C.                 D.1

    答案：B  令x=cosθ,y=sinθ,∴x+y=cosθ+sinθ=sin(θ+)≥m,即于任意θ恒成立,∴m≤ .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东省东营市2012届高三一模(3月)数学理科试题 题型：022

    已知定义在R上的偶函数满足：f(x＋4)＝f(x)＋f(2)，且当x∈[0，2]时，y＝f(x)单调递减，给出以下四个命题：

    ①f(2)＝0；

    ②x＝－4为函数y＝f(x)图象的一条对称轴；

    ③函数y＝f(x)在[8，10]单调递增；

    ④若方程f(x)＝m在[－6，－2]上的两根为x1、x2，则x1＋x2＝－8．

    以上命题中所有正确命题的序号为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系中，已知A1(-3,0)、A2(3,0),P(x,y),M(,0)，若实数λ使向量、λ、满足λ2·()2=·.

    (1)求P点的轨迹方程，并判断P点的轨迹是怎样的曲线；

    (2)当λ=时，过点A1且斜率为1的直线与(1)中的曲线相交的另一点为B，能否在直线x=-9上找一点C，使△A1BC为正三角形.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若x+y≥m时满足x2+y2=1的任意实数对(x,y)都成立，则m的最大值为

    A.0                    B.              C.                 D.1

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年黑龙江省哈尔滨三中高一（上）期末数学试卷（解析版） 题型：解答题

    已知函数f1（x）=lg|x-p1|，f2（x）=lg（|x-p2|+2）（x∈R，p1，p2为常数）
    函数f（x）定义为对每个给定的实数x（x≠p1），
    （1）当p1=2时，求证：y=f1（x）图象关于x=2对称；
    （2）求f（x）=f1（x）对所有实数x（x≠p1）均成立的条件（用p1、p2表示）；
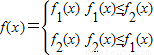
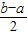    （3）设a，b是两个实数，满足a＜b，且p1，p2∈（a，b），若f（a）=f（b）求证：函数f（x）在区间[a，b]上单调增区间的长度之和为．（区间[m，n]、（m，n）或（m，n]的长度均定义为n-m）

    查看答案和解析>>

    同步练习册答案