
科目:高中数学 来源: 题型:
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长![]() 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于![]() 的函数
的函数![]() 的解析式;(6分 )
的解析式;(6分 )
 |
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?(6分 )
查看答案和解析>>
科目:高中数学 来源:2014届湖北省三校联考高一下学期期中理科联考数学试卷(解析版) 题型:解答题
某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。

【解析】本试题主要考查导数在研究函数中的运用。首先设变量
设宽为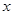 则长为
则长为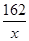 ,依题意,总造价
,依题意,总造价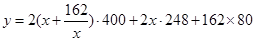
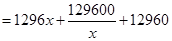
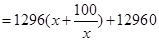
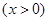
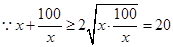 当且仅当
当且仅当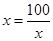 即
即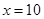 取等号
取等号
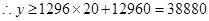 (元)得到结论。
(元)得到结论。
设宽为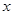 则长为
则长为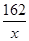 ,依题意,总造价
,依题意,总造价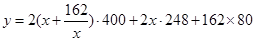
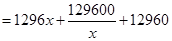
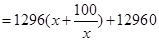
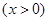 ………6分
………6分
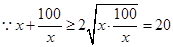 当且仅当
当且仅当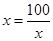 即
即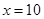 取等号
取等号
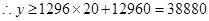 (元)……………………10分
(元)……………………10分
故当处理池宽为10米,长为16.2米时能使总造价最低,且最低总造价为38880元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com