
分析 (1)化简y=$\frac{1-{x}^{2}}{1+{x}^{2}}$=-1+$\frac{2}{1+{x}^{2}}$,从而求函数的值域;
(2)化简y=2x+$\sqrt{1-x}$=-2(1-x)+$\sqrt{1-x}$+2=-2($\sqrt{1-x}$-$\frac{1}{4}$)2+$\frac{17}{8}$,从而求函数的值域;
(3)利用换元法令x=sina,$\sqrt{1-{x}^{2}}$=cosa,(-$\frac{π}{2}$≤a≤$\frac{π}{2}$),从而化简求函数的值域;
(4)化简分离y=$\frac{{x}^{2}-2x+5}{x-1}$=(x-1)+$\frac{4}{x-1}$,从而求函数的值域;
(5)3x2+2y2=6x可化为(x-1)2+$\frac{2}{3}$y2=1;故令x=1+cosa,y=$\frac{\sqrt{6}}{2}$sina;从而化简求函数的值域;
(6)作函数f(x)=|2x+1|-|x-4|的图象,从而求函数的值域.
解答 解:(1)y=$\frac{1-{x}^{2}}{1+{x}^{2}}$=-1+$\frac{2}{1+{x}^{2}}$;
故函数的值域为(-1,1];
(2)y=2x+$\sqrt{1-x}$
=-2(1-x)+$\sqrt{1-x}$+2
=-2($\sqrt{1-x}$-$\frac{1}{4}$)2+$\frac{17}{8}$;
故函数的值域为{y|y≤$\frac{17}{8}$};
(3)y=2x+$\sqrt{1-{x}^{2}}$,
令x=sina,$\sqrt{1-{x}^{2}}$=cosa,(-$\frac{π}{2}$≤a≤$\frac{π}{2}$);
故y=2sina+cosa=$\sqrt{5}$sin(a+θ),
(其中sinθ=$\frac{\sqrt{5}}{5}$,cosθ=$\frac{2\sqrt{5}}{5}$);
故-2≤2x+$\sqrt{1-{x}^{2}}$≤$\sqrt{5}$;
故函数的值域为[-2,$\sqrt{5}$];
(4)y=$\frac{{x}^{2}-2x+5}{x-1}$=(x-1)+$\frac{4}{x-1}$;
故函数的值域为(-∞,-4]∪[4,+∞);
(5)3x2+2y2=6x可化为(x-1)2+$\frac{2}{3}$y2=1;
令x=1+cosa,y=$\frac{\sqrt{6}}{2}$sina;
故z=x2+y2=1+cos2a+2cosa+$\frac{3}{2}$sin2a
=-$\frac{1}{2}$(cosa-2)2+$\frac{9}{2}$;
∵1≤(cosa-2)2≤9;
∴0≤-$\frac{1}{2}$(cosa-2)2+$\frac{9}{2}$≤4;
故函数z=x2+y2的值域为[0,4];
(6)作函数f(x)=|2x+1|-|x-4|的图象如下,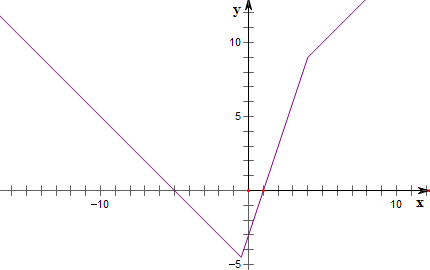
当x=-$\frac{1}{2}$时,y=-$\frac{9}{2}$;
故函数的值域为[-$\frac{9}{2}$,+∞).
点评 本题考查了函数的值域的求法,根据不同的问题选择不同的方法即可.


科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
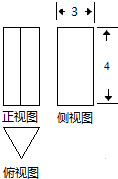 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )| A. | 18 | B. | 9$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com