
(1)f(x)=-8x2+7x+1;(2)f(x)=x2+x+2;
(3)f(x)=x3+1;(4)f(x)=![]() .
.
思路分析:本题主要考查函数的零点.可通过解方程求得函数的零点.
解:(1)因为f(x)=-8x2+7x+1=-(8x+1)(x-1),令f(x)=0可解得x=![]() ,或x=1,所以函数的零点为
,或x=1,所以函数的零点为![]() 和1.
和1.
(2)令x2+x+2=0,因为Δ=12-4×1×2=-7<0,所以方程无实数解,所以f(x)=x2+x+2不存在零点.
(3)因为f(x)=x3+1=(x+1)(x2-x+1),令(x+1)(x2-x+1)=0,解得x=-1,所以函数的零点为-1.
(4)因为f(x)=![]() ,令
,令![]() =0,解得x=-6,所以函数的零点为-6.
=0,解得x=-6,所以函数的零点为-6.
绿色通道:求函数的零点时,先考虑解方程f(x)=0,方程f(x)=0无根则函数无零点,方程f(x)=0有根则函数有零点.
黑色陷阱:本题(4)中解方程容易错写成函数的零点是-6,2,其原因是没有验根,避免出现此类错误的方法是解分式方程、对数方程等要验根,保证方程有意义.


科目:高中数学 来源: 题型:
| x2+4x-12 | x-2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2+4x-12 |
| x-2 |
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
判断下列函数是否存在零点,如果存在,请求出.
(1)f(x)=-8x2+7x+1;
(2)f(x)=x2+x+2;
(3)f(x)=x3+1;
(4)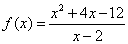 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com