函数y=log2(2cosx-1)的单调递减区间为________.
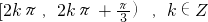
分析:先求出函数的定义域,函数y=log
2(2cosx-1)可看作由y=log
2t,t=2cosx-1复合而成的,因为y=log
2t单调递增,所以只需求出t=2cosx-1的减区间即可.
解答:由2cosx-1>0得-

+2kπ≤x≤

+2kπ,k∈Z,
所以函数的定义域为[-

+2kπ,

+2kπ](k∈Z),
函数y=log
2(2cosx-1)可看作由y=log
2t,t=2cosx-1复合而成的,
而y=log
2t单调递增,所以要求函数y=log
2(2cosx-1)的减区间,只需求t=2cosx-1的减区间即可.
t=2cosx-1的减区间为:[2kπ,

+2kπ](k∈Z).
故答案为:[2kπ,

+2kπ](k∈Z).
点评:本题考查复合函数的单调性,判断方法为“同增异减”,注意考虑函数定义域,单调区间必为定义域的子集.

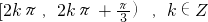
 +2kπ≤x≤
+2kπ≤x≤ +2kπ,k∈Z,
+2kπ,k∈Z, +2kπ,
+2kπ, +2kπ](k∈Z),
+2kπ](k∈Z), +2kπ](k∈Z).
+2kπ](k∈Z). +2kπ](k∈Z).
+2kπ](k∈Z).
