练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    ||＝2，||＝2，＝x＋y且x＋y＝1，∠AOB是钝角，f(t)＝|－t|的最小值为，则||的最小值为________．

    答案：1
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知某二次函数的图像与函数y＝2x2的图像的形状一样，开口方向相反，且其顶点为(－1,3)，则此函数的解析式为                                         (　　)

    A．y＝2(x－1)2＋3　　　　　         B．y＝2(x＋1)2＋3

    C．y＝－2(x－1)2＋3                 D．y＝－2(x＋1)2＋3

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年江西省鄱阳县油墩街中学高二下学期期中考试理科数学 题型：单选题

    若向量a＝(1，λ，2)，b＝(2，－1,2)，a、b的夹角的余弦值为8/9，则λ的值为(　　)

    A．2B．－2C．－2或2/55D．2或－2/55

    查看答案和解析>>

    科目：高中数学 来源：2011届湖北省天门市高三天5月模拟理科数学试题 题型：解答题

    已知数列{an}，且x＝是函数f(x)＝an－1x3－3[(t＋1)an－an＋1] x＋1(n≥2)的一个极值点．数列{an}中a1＝t，a2＝t2(t＞0且t≠1) ．
    （1）求数列{an}的通项公式；
    （2）记bn＝2(1－)，当t＝2时，数列{bn}的前n项和为Sn，求使Sn＞2010的n的最小值；
    （3）若cn＝，证明：( n∈N﹡)．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖北省天门市高三天5月模拟理科数学试题 题型：解答题

    已知数列{an}，且x＝是函数f(x)＝an－1x3－3[(t＋1)an－an＋1] x＋1(n≥2)的一个极值点．数列{an}中a1＝t，a2＝t2(t＞0且t≠1) ．

    （1）求数列{an}的通项公式；

    （2）记bn＝2(1－)，当t＝2时，数列{bn}的前n项和为Sn，求使Sn＞2010的n的最小值；

    （3）若cn＝，证明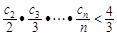：( n∈N﹡)．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知集合M＝{x|x2-4＝0，x∈R}，集合N＝{(x，y)|y＝x2-4，x、y∈R}，那么当y＝0时有


    1. A.
      M＝N＝{2，-2}
    2. B.
      M＝{2，-2}，N＝{(2，0)，(-2，0)}
    3. C.
      M＝N＝{(2，-2)}
    4. D.
      M＝{2，-2}，N＝{(2，-2)}

    查看答案和解析>>

    同步练习册答案