在计算“ 时.某同学学到了如下一种方法:先改写第K项:.由此得.相加.得.类比上述方法.请计算“ .其结果为. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

在计算“

（n∈N*）”时，某同学学到了如下一种方法：
先改写第K项：

，
由此得

，
相加，得

。
类比上述方法，请计算“

（n∈N*）”，其结果为（）。

练习册系列答案

学习总动员期末加暑假光明日报出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

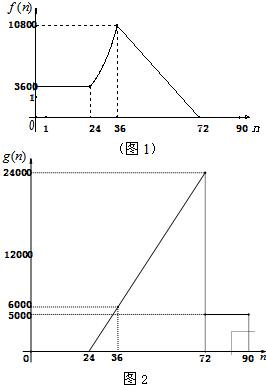2010年上海世博会组委会为保证游客参观的顺利进行，对每天在各时间段进入园区和离开园区的人数作了一个模拟预测．为了方便起见，以10分钟为一个计算单位，上午9点10分作为第一个计算人数的时间，即n=1；9点20分作为第二个计算人数的时间，即n=2；依此类推…，把一天内从上午9点到晚上24点分成了90个计算单位．
对第n个时刻进入园区的人数f（n）和时间n（n∈N^*）满足以下关系（如图1）：f（n）=

3600

(1≤n≤24)

3600•3

n-24

(25≤n≤36)

-300n+21600

(37≤n≤72)

(73≤n≤90)

，n∈N^*
对第n个时刻离开园区的人数g（n）和时间n（n∈N^*）满足以下关系（如图2）：g（n）=

0	(1≤n≤24)
500n-12000	(25≤n≤72)
5000	(73≤n≤90)

，n∈N^*
（1）试计算在当天下午3点整（即15点整）时，世博园区内共有多少游客？
（2）请求出当天世博园区内游客总人数最多的时刻．

查看答案和解析>>

科目：高中数学 来源： 题型：

在计算“1×2+2×3+…+n（n+1）”时，有如下方法：
先改写第k项：k（k+1）=

[k（k+1）（k+2）-（k-1）k（K+1）]，
由此得：1×2=

（1×2×3-0×1×2），
2×3=

（2×3×4-1×2×3），…，
n（n+1）=

[n（n+1）（n+2）-（n-1）n（n+1）]，
相加得：1×2+2×3+…+n（n+1）=

n（n+1）（n+2）．
类比上述方法，请你计算“1×3+2×4+…+n（n+2）”，其结果写成关于n的一次因式的积的形式为：

n（n+1）（2n+7）

．

查看答案和解析>>

科目：高中数学 来源： 题型：

在计算“1×2+2×3+…n（n+1）”时，先改写第k项：
k（k+1）=

[k（k+1）（k+2）-（k-1）k（k+1）]，由此得1×2=

（1×2×3-0×1×2），2×3=

（2×3×4-1×2×3），．．
n（n+1）=

[n（n+1）（n+2）-（n-1）n（n+1）]，相加，得1×2+2×3+…+n（n+1）=

n(n+1)(n+2)
（1）类比上述方法，请你计算“1×2×3+2×3×4+…+n（n+1）（n+2）”的结果；
（2）试用数学归纳法证明你得到的等式．

查看答案和解析>>

科目：高中数学 来源： 题型：

某国采用养老储备金制度，公民在就业的第一年就交纳养老储备金，数目为a₁，以后每年交纳的数目均比上一年增加d（d＞0），因此，历年所交纳的储备金数目a₁，a₂，…是一个公差为d的等差数列．与此同时，国家给予优惠的计息政府，不仅采用固定利率，而且计算复利．这就是说，如果固定年利率为r（r＞0），那么，在第n年末，第一年所交纳的储备金就变为a₁（1+r）^n-1，第二年所交纳的储备金就变成a₂（1+r）^n-2，…．以T_n表示到第n年末所累计的储备金总额．
（Ⅰ）写出T_n与T_n-1（n≥2）的递推关系式；
（Ⅱ）求证T_n=A_n+B_n，其中{A_n}是一个等比数列，{B_n}是一个等差数列．

查看答案和解析>>

科目：高中数学 来源：江西省临川二中、新余四中2012届高三第一次联考数学文科试题 题型：022

在计算“1×2＋2×3＋…＋n(n＋1)”时，某同学学到了如下一种方法：先改写第k项：k(k＋1)＝[k(k＋1)(x＋2)－(k－1)k(k＋1)]，由此得