
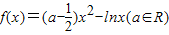
 )x2+lnx-2a<0恒成立,只要求出(a-
)x2+lnx-2a<0恒成立,只要求出(a- )x2+lnx-2a的最大值小于0即可,我们可以令一个新的函数,然后利用导数研究其最值问题,从而求解;
)x2+lnx-2a的最大值小于0即可,我们可以令一个新的函数,然后利用导数研究其最值问题,从而求解; x2-lnx(a∈R)
x2-lnx(a∈R)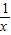 =
=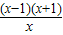 (x>0)
(x>0) ;
; )x2+lnx-2a<0恒成立,
)x2+lnx-2a<0恒成立, )x2+lnx-2a,x∈(1,+∞),
)x2+lnx-2a,x∈(1,+∞),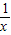 =(x-1)(2a-1-
=(x-1)(2a-1-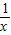 )
)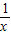 <1,
<1,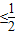 ,g′(x)<0,函数g(x)在区间[1,+∞)上位减函数,
,g′(x)<0,函数g(x)在区间[1,+∞)上位减函数, -2a=-
-2a=- -a,只需要
-a,只需要 -a≤0,即当-
-a≤0,即当- ≤a≤
≤a≤ 时,g(x)=(a-
时,g(x)=(a- )x2+lnx-2ax<0恒成立;
)x2+lnx-2ax<0恒成立; <a<1时,令g′(x)=(x-1)(2a-1-
<a<1时,令g′(x)=(x-1)(2a-1-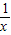 )=0,
)=0,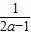 >1,函数g(x)在区间(1,
>1,函数g(x)在区间(1,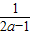 )为减函数,在(
)为减函数,在(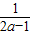 ,+∞)上位增函数,
,+∞)上位增函数,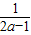 ),+∞),不合题意;
),+∞),不合题意; ≤a
≤a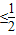 时,g(x)=(a-
时,g(x)=(a- )x2+lnx-2ax<0恒成立;
)x2+lnx-2ax<0恒成立; ≤a
≤a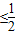 时,在区间(1,+∞)上函数f(x)的图象恒在直线y=2ax的下方;
时,在区间(1,+∞)上函数f(x)的图象恒在直线y=2ax的下方;

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:2012-2013学年山东省高三上学期期末模块考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数
(I)当a=1时,求函数 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;
(II)当a=2时,在 的条件下,求
的条件下,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市高三上学期期中考试数学(解析版) 题型:解答题
(本题满分16分)
已知函数
(I)当a=2时,求函数 的最大值和最小值;
的最大值和最小值;
(II)若函数 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(III)当a=1时,求证:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省唐山市高三下学期第二次模拟考试数学理卷 题型:解答题
(本小题满分12分)
已知函数
(I)当a=1时,求 的最小值;
的最小值;
(II)求证: 在区间(0,1)单调递减。
在区间(0,1)单调递减。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com