解:(1)函数的定义域为(0,+∞)
求导函数可得

∵函数f(x)=ax-
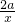
-61nx在x=2处取得极值,
∴f′(2)=0,即

=0,∴a=2
当a=2时,

x∈(1,2)时,f′(x)<0;x∈(2,+∞),f′(x)>0
∴函数f(x)在x=2处取得极值,∴a=2;
(2)由(1)知

,

∴当x∈(0,1)时,f′(x)>0,f(x)在(0,1)上是增函数;当x∈(1,2)时,f′(x)<0,f(x)在(1,2)上是减函数
∴f(x)在(0,2)上的最大值为f(1)=-2
∵g(x)=(x-3)e
x-m,∴g′(x)=(x-2)e
x≥0在[2,3]上恒成立
∴g(x)在[2,3]上单调递增,其值域为[-e
2-m,-m]
∵对任意x
1∈(0,2),x
2∈[2,3],总有f(x
1)-g(x
2)≤0成立,
∴f(x)
max≤g(x)
min,
∴-2≤-e
2-m
∴m≤2-e
2.
分析:(1)确定函数的定义域,求导函数,利用极值的定义,即可求实数a的值;
(2)对任意x
1∈(0,2),x
2∈[2,3],总有f(x
1)-g(x
2)≤0成立,等价于f(x)
max≤g(x)
min,求出最值,即可得到结论.
点评:本题考查导数知识的运用,考查函数的极值,考查恒成立问题,对任意x
1∈(0,2),x
2∈[2,3],总有f(x
1)-g(x
2)≤0成立,转化为f(x)
max≤g(x)
min,是解题的关键.

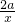 -61nx在x=2处取得极值.
-61nx在x=2处取得极值.
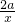 -61nx在x=2处取得极值,
-61nx在x=2处取得极值, =0,∴a=2
=0,∴a=2
 ,
,

