(Ⅰ)解:对任意x∈[0,1],f
1(x)=x≥0,且f
1(0)=0,f
1(1)=1,满足条件①;
对满足条件0≤x
1≤1,0≤x
2≤1,0≤x
1+x
2≤1的任意两个数x
1,x
2,f
1(x
1+x
2)=x
1+x
2≥f
1(x
1)+f
1(x
2)=x
1+x
2,满足条件②.
故f
1(x)=x是Γ函数;
对任意x∈[0,1],f
2(x)=sin

x≥0成立,且f
2(0)=0,f
2(1)=1,满足条件①;
但取x
1=1,x
2=2时,f
2(x
1+x
2)=sin
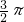
=-1,f
2(x
1)+f
2(x
2)=sin

+sinπ=1,f(x
1+x
2)<f(x
1)+f(x
2),不满足条件②,
故f
2(x)=sin

x不是Γ函数;
(Ⅱ)证明:对于任意的0≤x≤y≤1,
则0≤y-x≤1,∴f(y-x)≥0.
∴f(y)=f(y-x+x)≥f(y-x)+f(x)≥f(x).
∴对于任意的0≤x≤y≤1,有f(x)≤f(y).
(Ⅲ)不都成立,证明如下:
取函数

,
则f(x)显然满足题目中的(1),(2)两个条件.
任意取两个数x
1,x
2,使得x
1≥0,x
2≥0,x
1+x
2≤1,
若x
1,x
2∈[0,1],则f(x
1+x
2)≥0=f(x
1)+f(x
2).
若x
1,x
2分别属于区间[0,

]和(

,1]中一个,则f(x
1+x
2)=1=f(x
1)+f(x
2),
而x
1,x
2不可能都属于(

,1].
综上可知,f(x)满足题目中的三个条件.
而f(0.51)=1>1.5×0.51=0.785.
即不等式f(x)≤

x并不对所有x∈[0,1]都成立.
分析:(Ⅰ)按照Γ函数的定义逐个验证即可;
(Ⅱ)欲证对于任意的0≤x≤y≤1,有f(x)≤f(y),将y写成y-x+x,利用f(x
1+x
2)≥f(x
1)+f(x
2)进行放缩即得.
(Ⅲ)取函数

,验证此函数符合题目中的条件(1),(2),但是f(0.51)=1>1.5×0.51=0.785.从而不等式f(x)≤

x并不对所有x∈[0,1]都成立.
点评:本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题.

 x是否为Γ函数,并说明理由;
x是否为Γ函数,并说明理由; x对于一切x∈[0,1]都成立吗?证明你的结论.
x对于一切x∈[0,1]都成立吗?证明你的结论. x≥0成立,且f2(0)=0,f2(1)=1,满足条件①;
x≥0成立,且f2(0)=0,f2(1)=1,满足条件①;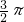 =-1,f2(x1)+f2(x2)=sin
=-1,f2(x1)+f2(x2)=sin +sinπ=1,f(x1+x2)<f(x1)+f(x2),不满足条件②,
+sinπ=1,f(x1+x2)<f(x1)+f(x2),不满足条件②, x不是Γ函数;
x不是Γ函数; ,
, ]和(
]和( ,1]中一个,则f(x1+x2)=1=f(x1)+f(x2),
,1]中一个,则f(x1+x2)=1=f(x1)+f(x2), ,1].
,1]. x并不对所有x∈[0,1]都成立.
x并不对所有x∈[0,1]都成立. ,验证此函数符合题目中的条件(1),(2),但是f(0.51)=1>1.5×0.51=0.785.从而不等式f(x)≤
,验证此函数符合题目中的条件(1),(2),但是f(0.51)=1>1.5×0.51=0.785.从而不等式f(x)≤ x并不对所有x∈[0,1]都成立.
x并不对所有x∈[0,1]都成立.
