
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.

(1)求证:PC⊥AB;
(2)求二面角B-AP-C的大小.
(3)求点C到平面APB的距离.
|
解法一: (1)取AB中点D,连结PD,CD. ∵AP=BP, ∴PD⊥AB. ∵AC=BC. ∴CD⊥AB 2分 ∵PD∩CD=D. ∴AB⊥平面PCD 3分 ∵PC ∴PC⊥AB 4分 (2)∵AC=BC,AP=BP, ∴△APC≌△BPC. ∴PC⊥AC, ∴PC⊥BC. 又∠ACB=90°,且AC∩PC=C, ∴BC⊥平面PAC. 取AP中点E,连结BE,CE.
∴AB=BP, ∴BE⊥AP. ∵CE是BE在平面PAC内的射影, ∴CE⊥AP. ∴∠BEC是二面角B-AP-C的平面角 6分 在△BCE中,∠BCE=90°,BC=2,BE= ∴sin∠BEC= ∴二面角B-AP-C的大小为aresin (4)在Rt△ABC中,∵AC=BC=2,∠ABC=90°,∴AB= 由已知,得AP=BP= 解法二: (1)如图,以C为原点建立空间直角坐标系C-xyz. 则C(0,0,0),A(0,2,0),B(2,0,0). 设P(0,0,t), 2分
∵|PB|=|AB|=2 ∴t=2,P(0,0,2) ∴PC⊥AB 4分 (2)取AP中点E,连结BE,CE. ∵|AC|=|PC|,|AB|=|BP| 6分 ∴∠BEC是二面角B-AP-C的平面角. ∵E(0,1,1), ∴cos∠BEC= ∴二面角B-AP-C的大小为arccos (3)∵AC=BC=PC, ∴C在平面APB内的射影为正△APB的中心H,且CH的长为点C到平面APB的距离. ∴点C到平面APB的距离为 |


科目:高中数学 来源: 题型:
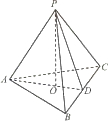 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2查看答案和解析>>
科目:高中数学 来源: 题型:
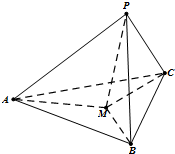 如图,在三棱锥P-ABC中,PA,PB,PC两两垂直,且PA=5,PB=4,PC=3.设点M为底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别为三棱锥M-PAB、M-PBC、M-PCA的体积.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,则正实数a的取值范围是
如图,在三棱锥P-ABC中,PA,PB,PC两两垂直,且PA=5,PB=4,PC=3.设点M为底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别为三棱锥M-PAB、M-PBC、M-PCA的体积.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,则正实数a的取值范围是查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.| 1 |
| 2 |
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
| z1+z2+z3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•莆田模拟)如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A、B为直角顶点的等腰直角三角形,AB=1.
(2012•莆田模拟)如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A、B为直角顶点的等腰直角三角形,AB=1.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com