练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    光线沿直线y=2x+1的方向射在直线y=x上.求反射后的光线所在的直线方程.

    思路解析：根据光学知识，入射角等于反射角，可以根据夹角公式求解，也可以利用对称来求解,后一种更方便.

    解法一：设P（x，y）是反射后的光线所在直线上任意一点，由光学知识可知P关于y=x的对称点P′（x0，y0）在直线y=2x+1上，∴y0=2x0+1.

    而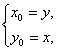所以反射光线所在的直线方程为x=2y+1，即x-2y-1=0.

    事实上，只需将y=2x+1中的x，y对调，便可得出此曲线关于直线y=x的对称曲线的方程.

    解法二：解方程组得交点P（-1，-1）.

    在直线y=2x+1上任取一点A（1，3），A点关于直线y=x的对称点B（3，1）必在反射光线所在的直线上，

    ∴反射光线的方程为PB：=，即x-2y-1=0.

    解法三：由方程组得交点P（-1，-1）.过P点且垂直直线y=x的直线方程为x+y+2=0.

    由光学知识可知入射线与反射线关于直线x+y+2=0对称.

    在y=2x+1上任取一点C（0，1），关于直线x+y+2=0的对称点为D（-3，-2）.

    直线PD：=，即x-2y-1=0为反射光线所在直线的方程.

    解法四：解方程组得交点P（-1，-1）.

    设直线y=x到y=2x+1的角为α，则tanα==.

    设反射光线所在直线的斜率为k,则=，则k=，则反射光线所在直线的方程为y+1=（x+1），即x-2y-1=0.

    解法五：在y=2x+1上任取两点A（0，1）、B（-1，-1），它们关于y=x的对称点为A′（1，0）、B′（-1，-1）.A′B′所在的直线方程为=，即x-2y-1=0为反射光线所在的直线方程.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    光线沿直线y=2x+1射到直线y=x上，被直线y=x反射后的光线所在的直线方程为（　　）
    A、y=
    1
    2
    x-1
    B、y=
    1
    2
    x-
    1
    2
    C、y=
    1
    2
    x+
    1
    2
    D、y=
    1
    2
    x+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    7、入射光线沿直线y=2x+1射向直线y=x，被y=x反射后，反射光线所在的直线方程是
    x-2y-1=0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设入射光线沿直线y=2x+1射向直线y=x，则被y=x反射后，反射光线所在的直线方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    光线沿直线y=2x+1入射到直线x+y+5=0后反射，则反射光线所在直线方程为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    光线沿直线y=2x+1射到直线y=x上，被y=x反射后的光线所在的直线方程为

    A.y=x-1                           B.y=x-

    C.= x+                        D.y=x+1

    查看答案和解析>>

    同步练习册答案