
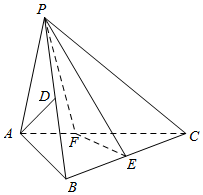
 如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,已知PA=AB,∠ABC为直角,PA⊥BC.点D,E分别为PB,BC的中点.分析 (1)证明:BC⊥AD,AD⊥PB,即可证明AD⊥平面PBC;
(2)当AM∥EF,即$\frac{AF}{FC}$=$\frac{1}{2}$时,可得平面ADM∥平面PEF,即可得出结论.
解答  (1)证明:∵∠ABC为直角,PA⊥BC,
(1)证明:∵∠ABC为直角,PA⊥BC,
∴BC⊥平面PAB,
∵AD?平面PAB,
∴BC⊥AD,
∵PA=AB,D是PB的中点,
∴AD⊥PB,
∵PB∩BC=B,
∴AD⊥平面PBC;
(2)解:取BE的中点M,则PE∥DM,
当AM∥EF,即$\frac{AF}{FC}$=$\frac{1}{2}$时,可得平面ADM∥平面PEF,∴AD∥平面PEF,
故$\frac{AF}{FC}$=$\frac{1}{2}$时,AD∥平面PEF.
点评 本题考查线面垂直、平行的证明,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>n且e1e2>1 | B. | m>n且e1e2<1 | C. | m<n且e1e2>1 | D. | m<n且e1e2<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
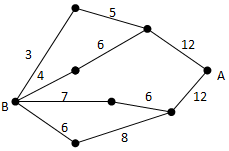 如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )
如图,小黑圆表示网络的结点,结点之间的连线表示它们有网线相连.连线上标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递.则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,3} | B. | {1,2,3} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com