
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先根据函数y=f(x)(x∈R)满足f(x-1)=f(x+1),f(x+2)=f(x),得出f(x)是周期为2的周期性函数,再把函数的零点转化为两函数图象的交点,利用图象直接得结论.
解答 解:∵函数y=f(x)(x∈R)满足f(x-1)=f(x+1),
∴f(x+2)=f(x),f(x)是周期为2的周期性函数,
又x∈[-1,1]时,f(x)=x2.
根据函数的周期性画出图形,如图,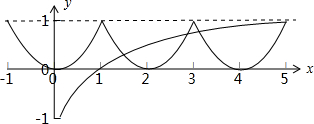
由图可得y=f(x)与y=log5x的图象有4个交点.
故选:C.
点评 本题考查函数的零点,求解本题,关键是研究出函数f(x)性质,作出其图象,将函数y=f(x)-log5x的零点个数的问题转化为两个函数交点个数问题是本题中的一个亮点,此一转化使得本题的求解变得较容易.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{8}$-x2=1 | B. | x2-$\frac{y^2}{8}$=1 | C. | x2-$\frac{y^2}{8}$=1(x≥1) | D. | x2-$\frac{y^2}{8}$=1(x≤-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com