
已知函数f(x)=alnx+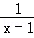 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x2)﹣f(x1)≥ln2+
,2]时,求证:f(x2)﹣f(x1)≥ln2+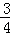 .
.
(1)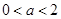 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查导数的运算,利用导数研究函数的单调性及最值、不等式等基础知识,考查函数思想,突出考查综合运用数学知识和方法分析问题解决问题的能力.第一问,先对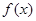 求导,由函数
求导,由函数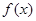 定义域可知,
定义域可知,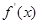 的分母为正数,设
的分母为正数,设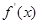 的分子为新函数
的分子为新函数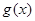 ,判断
,判断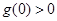 ,所以
,所以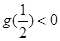 或
或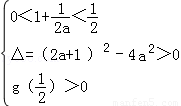 ,解得
,解得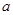 的取值范围;第二问,对
的取值范围;第二问,对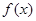 求导,令
求导,令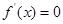 ,设出方程的两根,利用韦达定理得到两根之和、两根之积,判断导函数的正负,决定函数
,设出方程的两根,利用韦达定理得到两根之和、两根之积,判断导函数的正负,决定函数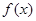 的单调性,求出最大值和最小值,代入求证的式子的左边,化简,得到
的单调性,求出最大值和最小值,代入求证的式子的左边,化简,得到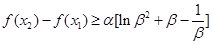 ,再求函数
,再求函数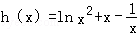 的最小值,通过不等式的传递性得到求证的表达式.
的最小值,通过不等式的传递性得到求证的表达式.
试题解析: (I)由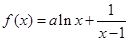 (
(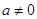 ),得:
),得: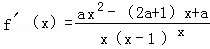 ,
,
∵a≠0,令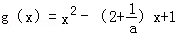 ,∴
,∴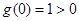 .
.
令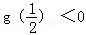 或
或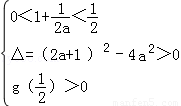 , 则
, 则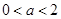 .
.
(II)由(I)得: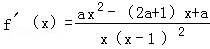 ,
,
设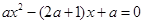 (
(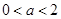 )的两根为
)的两根为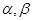 ,
,
则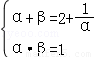 ,得
,得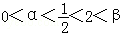 .
.
当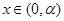 和
和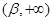 时,
时,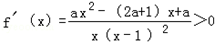 ,函数f(x)单调递增;
,函数f(x)单调递增;
当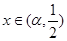 和
和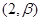 时,
时,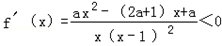 ,函数f(x)单调递减,
,函数f(x)单调递减,
则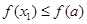 ,
,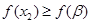 ,
,
则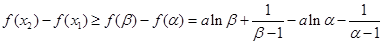
=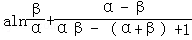 =
=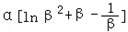 (利用
(利用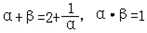 )
)
令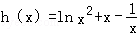 ,
,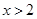 则
则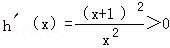 ,
,
则函数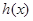 单调递增,
单调递增, 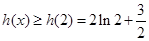 ,
,
∴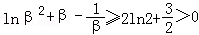 ,
,
∵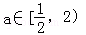 ,则
,则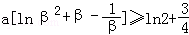 ,
,
∴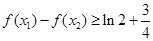 .
.
考点:1.二次函数的性质;2.零点问题;3.利用导数判断函数的单调区间;4. 利用导数判断函数的最值;5.不等式的性质.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com