
分析 (Ⅰ)得到|PM|=|PF|,求出点P的轨迹是椭圆,其中2a=4,c=$\sqrt{3}$,求出椭圆方程即可;
(Ⅱ)求出SAFBD=2S△AFB,通过讨论AB是短轴、AB是长轴的情况,求出四边形的面积即可.
解答 解:(Ⅰ)由于点P为线段MF的垂直平分线,
故|PM|=|PF|,
故|PE|+|PF|=|PE|+|PM|=|ME|=4>2$\sqrt{3}$,
故点P的轨迹是椭圆,其中2a=4,c=$\sqrt{3}$,
因此P点的轨迹C的方程是:$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)由$\overrightarrow{FD}$=$\overrightarrow{FA}$+$\overrightarrow{FB}$,知四边形AFBD是平行四边形,
故SAFBD=2S△AFB,
(1)AB是短轴时,
S△AFB=$\frac{1}{2}$|AB|•|OF|=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$
即SAFBD=2$\sqrt{3}$;
(2)AB是长轴时,易知AFBD不是四边形,故AB斜率不是0;
(3)直线AB的斜率存在且不是0时,设其斜率为k,
则直线AB的方程是:y=kx(k≠0),
设A(x1,y1),B(x2,y2),
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}{+y}^{2}=1}\\{y=kx}\end{array}\right.$,消去x得:
(1+4k2)y2-4k2=0,
故y1+y2=0,y1y2=$\frac{-{4k}^{2}}{1+{4k}^{2}}$,
SAFBD=2S△ABF=2×$\frac{1}{2}$|OF|•|y1-y2|=$\sqrt{3}$•$\sqrt{{{(y}_{1}{+y}_{2})}^{2}-{{4y}_{1}y}_{2}}$=$\sqrt{3}$•$\sqrt{\frac{1{6k}^{2}}{1+{4k}^{2}}}$=$\frac{4\sqrt{3}}{\sqrt{\frac{1}{{k}^{2}}+4}}$,
而$\frac{1}{{k}^{2}}$+4>4,故0<$\frac{4\sqrt{3}}{\sqrt{\frac{1}{{k}^{2}}+4}}$<$\frac{4\sqrt{3}}{\sqrt{4}}$=2$\sqrt{3}$,
综上,四边形AFBD的面积的取值范围是(0,2$\sqrt{3}$].
点评 本题考查了椭圆的轨迹方程,考查分类讨论思想以及转化思想,是一道中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$) | B. | [0,2] | C. | [1,2) | D. | [1,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\sqrt{5},2\sqrt{5}]$ | B. | $[\sqrt{5},2\sqrt{10})$ | C. | $(\sqrt{5},\sqrt{10})$ | D. | $[\sqrt{5},2\sqrt{10}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
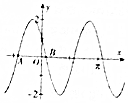 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图.
每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图.| 本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 频数 | 3 | 1 | 8 | 4 | 2 | 2 |
| 性别 阅读量 | 丰富 | 不丰富 | 合计 |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {8,10} | B. | {8,12} | C. | {8,14} | D. | {8,10,14} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10-ln3 | B. | 8-ln3 | C. | $\frac{22}{3}$ | D. | $\frac{64}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com