Question

16．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是梯形，其中AD∥BC，BA⊥AD，AC与BD交于点O，M是
AB边上的点，且AM=2BM，已知PA=AD=4，AB=3，BC=2．
（1）求平面PMC与平面PAD所成锐二面角的正切；
（2）已知N是PM上一点，且ON∥平面PCD，求$\frac{PN}{PM}$的值．

Answer 1

分析 解法1：（1）连接CM并延长交DA的延长线于E，说明∠MFA是平面PMC与平面PAD所成锐二面角的平面角然后求解tan∠MFA=$\frac{MA}{FA}$=$\frac{{\sqrt{2}}}{2}$，得到结果．
（2）连接MO并延长交CD于G，连接PG，在△BAD中，通过$\frac{BO}{OD}=\frac{BC}{AD}=\frac{1}{2}$，说明MO∥AD，然后求解$\frac{PN}{PM}$的值．
解法2 （1）以A为坐标原点，AB、AD、AP为x．y，z轴建立如图所示直角坐标系，求出平面PMC的法向量，平面PAD的法向量，通过向量的数量积求解平面PMC与平面PAD所成锐二面角的正切．
（2）求出平面PCD的法向量，设$\overrightarrow{PN}$=λ$\overrightarrow{PM}$，然后求解即可．

解答 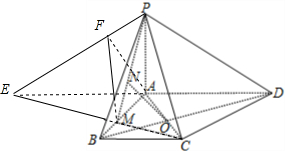解法1：（1）连接CM并延长交DA的延长线于E，则
PE是平面PMC与平面PAD所成二面角的棱，
过A作AF垂直PE于F，连接MF．
∵PA⊥平面ABCD，∴PA⊥MA，
又MA⊥AD，∴MA⊥平面PAD，
∵AF⊥PE，∴MF⊥PE，
∴∠MFA是平面PMC与平面PAD
所成锐二面角的平面角…（3分）
∵BC=2，AD=4，BC∥AD，AM=2MB
∴AE=4，又PA=4，∴AF=$2\sqrt{2}$
∴tan∠MFA=$\frac{MA}{FA}$=$\frac{{\sqrt{2}}}{2}$，
所以平面PMC与平面PAD所成锐二面角的正切为$\frac{{\sqrt{2}}}{2}$…（6分）
（2）连接MO并延长交CD于G，连接PG
∵ON∥平面PCD，∴ON∥PG
在△BAD中∵$\frac{BO}{OD}=\frac{BC}{AD}=\frac{1}{2}$，又$\frac{BM}{MA}=\frac{1}{2}$
∴$\frac{BO}{OD}=\frac{BM}{MA}$∴MO∥AD …（9分）
又在直角梯形ABCD中，MO=OG=$\frac{4}{3}$，
∵ON∥PG∴PN=MN，∴$\frac{PN}{PM}=\frac{1}{2}$…（12分）
解法2 （1）以A为坐标原点，AB、AD、AP为x．y，z轴建立如图所示直角坐标系，
则A（0，0，0）、B（3，0，0）、C（3，2，0）、D（0，4，0）、M（2，0，0）、P（0，0，4）、O（2，4/3，0）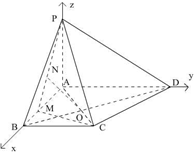
            
设平面PMC的法向量是$\overrightarrow u$=（x，y，z），则
∵$\overrightarrow{MC}$=（1，2，0），$\overrightarrow{MP}$=（-2，0，4）∴$\left\{\begin{array}{l}x+2y=0\\-2x+4z=0\end{array}\right.$令y=-1，则x=2，z=1
∴$\overrightarrow u$=（2，-1，1）
又AB⊥平面PAD，∴$\overrightarrow v$=（1，0，0）是平面PAD的法向量∴$cosθ=|\frac{\overrightarrow u•\overrightarrow v}{{|{\overrightarrow u}||{\overrightarrow v}|}}|=\sqrt{\frac{2}{3}}$∴$tanθ=\frac{{\sqrt{2}}}{2}$
所以平面PMC与平面PAD所成锐二面角的正切为$\frac{{\sqrt{2}}}{2}$…（6分）
（2）设平面PCD的法向量 $\overrightarrow{v'}$=（x’，y’，z’）
∵$\overrightarrow{PC}$=（3，2，-4），$\overrightarrow{PD}$=（0，4，-4）
∴$\left\{\begin{array}{l}3x'+2y'-4z'=0\\ 4y'-4z'=0\end{array}\right.$令y'=3，则x'=2，z'=3
∴$\overrightarrow{v'}=（{2，3，3}）$
设$\overrightarrow{PN}$=λ$\overrightarrow{PM}$，则∵$\overrightarrow{PM}$=（2，0，-4）∴$\overrightarrow{PN}$=（2λ，0，-4λ）$\overrightarrow{ON}$=$\overrightarrow{AN}-\overrightarrow{AO}=\overrightarrow{AP}+\overrightarrow{PN}-\overrightarrow{AO}$=（2λ-2，-4/3，4-4λ）
∵$\overrightarrow{ON}$⊥$\overrightarrow{v'}$∴4λ-4-4+12-12λ=0
∴$λ=\frac{1}{2}$，∴$\frac{PN}{PM}=\frac{1}{2}$…（12分）

点评 本题考查二面角的平面角的求法，几何法与向量法的应用，考查空间想象能力以及计算能力．