
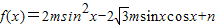 ,(m>0)的定义域为
,(m>0)的定义域为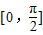 ,值域为[-5,4].
,值域为[-5,4].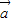 平移后关于原点中心对称,求向量
平移后关于原点中心对称,求向量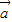 的坐标.
的坐标.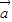 的坐标.
的坐标.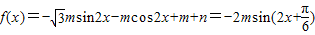 +m+n,
+m+n,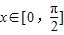
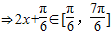
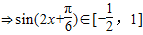 ,(4分)
,(4分)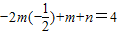 ,f(x)min=-m+n=-5
,f(x)min=-m+n=-5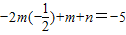
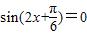 ,解得
,解得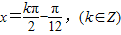 ,(10分)
,(10分)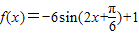 ,
,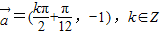 (12分)
(12分)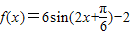 ,
,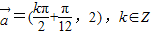 (14分)
(14分)

科目:高中数学 来源:湖南省浏阳一中2010-2011学年高一第一次阶段性考试数学试题 题型:044
已知函数![]()
(1)当m=0时,求f(x)在区间![]() 上的取值范围;
上的取值范围;
(2)当tana=2时,![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:高中数学 来源:辽宁省辽南协作体2012届高三上学期期中考试数学文科试题 题型:044
已知函数![]() ,其中m<0.
,其中m<0.
(Ⅰ)若f(x)的单调增区间是(0,1),求m的值;
(Ⅱ)当![]() 时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市德化一中高二(下)第二次质检数学试卷(文科)(解析版) 题型:解答题
 ,其中m>0.
,其中m>0.查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市徐汇区位育中学高三(上)期中数学试卷(文科)(解析版) 题型:解答题
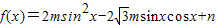 ,(m>0)的定义域为
,(m>0)的定义域为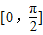 ,值域为[-5,4].
,值域为[-5,4].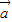 平移后关于原点中心对称,求向量
平移后关于原点中心对称,求向量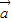 的坐标.
的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com