
 (n≥3).令bn=
(n≥3).令bn= ,且已知f(x)=2x-1.
,且已知f(x)=2x-1. ;
; .
. •2n-1=
•2n-1= •
• =
= (
(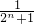 -
-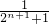 )…(6分)
)…(6分) [(
[( -
- )+(
)+( -
- )+…+(
)+…+(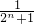 -
-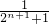 )]
)] (
( -
-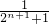 )
) •
• =
= .…(7分)
.…(7分) +
+ +
+ +…+
+…+ =
= +
+ +…+
+…+ ,
, +
+ +…+
+…+ ≥n
≥n …(8分)
…(8分) +
+ +…+
+…+ ≥n
≥n …(10分)
…(10分) +
+ +…+
+…+ )•(
)•( +
+ +…+
+…+ )≥n2,
)≥n2, +
+ +…+
+…+ )•(n+1-
)•(n+1- )≥n2,…(11分)
)≥n2,…(11分) +
+ +…+
+…+ ≥
≥ >
>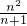 …(12分)
…(12分) >
> 成立,
成立, +
+ >
> 成立;…(8分)
成立;…(8分) >
> 成立,本问不得分)
成立,本问不得分) +
+ +…+
+…+ >
> 成立,
成立, +
+ +…+
+…+ +
+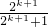 >
> +
+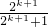 ,
, +
+ +…+
+…+ +
+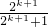 >
> ,
, +
+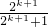 >
> ,
,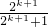 >
> -
- ,
,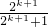 >
> …(9分)
…(9分)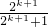 >
> ,
, >1-
>1- ,
, +2
+2 +2
+2 +1=k2+3k+3>(k+1)(k+2)…(11分)
+1=k2+3k+3>(k+1)(k+2)…(11分) •2n-1转化为bnf(n)=
•2n-1转化为bnf(n)= (
(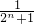 -
-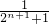 ),求和时再利用放缩法即可证得Tn=b1f(1)+b2f(2)+…+bnf(n)<
),求和时再利用放缩法即可证得Tn=b1f(1)+b2f(2)+…+bnf(n)< ;
; +
+ +
+ +…+
+…+ =
= +
+ +…+
+…+ ,利用基本不等式可证明(
,利用基本不等式可证明( +
+ +…+
+…+ )•(
)•( +
+ +…+
+…+ )≥n2,再对
)≥n2,再对 +
+ +…+
+…+ 通过分离常数得到n+1-
通过分离常数得到n+1- ,放缩后即可得证结论;
,放缩后即可得证结论; >
> 成立,
成立, +
+ +…+
+…+ >
> 成立,
成立,

科目:高中数学 来源: 题型:
| n+1 |
| 2 |
| 2n |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com