已知函数f(x)的定义域为R,对任意实数m,n都有f(m+n)=f(m)•f(n)且当x>0时,0<f(x)<1.
(1)证明f(0)=1,且x<0时,f(x)>1;
(2)证明f(x)在R上单调递减.
证明:(1)令m=1,n=0,代入f(m+n)=f(m)•f(n)中得:
f(1+0)=f(1)•f(0),即f(1)=f(1)•f(0),
∵1>0,
∴0<f(1)<1,
∴f(0)=1…2分
当x<0时,-x>0,故得0<f(-x)<1,令m=x,n=-x,则m+n=0,代入f(m+n)=f(m)•f(n)中得:
f(x)•f(-x)=f(0)=1,
∴f(x)=
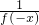
>1…6分
(2)设x
1<x
2,则x
2-x
1>0且0<f(x
2-x
1)<1,f(x
1)>0,
∴f(x
2)-f(x
1)=f(x
2-x
1+x
1)-f(x
1)
=f(x
2-x
1)•f(x
1)-f(x
1)
=f(x
1)[f(x
2-x
1)-1],
∵x
2-x
1>0,
∴f(x
2-x
1)<1,
∴f(x
2-x
1)-1<0,
∴f(x
2)-f(x
1)<0,
∴f(x
1)>f(x
2),
∴f(x)在R上单调递减.
分析:(1)令m=1,n=0,代入f(m+n)=f(m)•f(n)即可;
(2)利用单调函数的定义,设x
1<x
2,判断f(x
2)-f(x
1)<0即可.
点评:本题考查抽象函数及其应用,考查函数单调性的判断与证明,着重考查单调函数的定义的应用,属于难题.

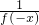 >1…6分
>1…6分

