【答案】
分析:(1)将n=1代入已知递推式,易得a
2,从而求出d,故a
n可求;
(2)求出b
n,分p=1和p≠1两种情况讨论,然后利用错位相减法求和.
解答:解:(Ⅰ)设等差数列{a
n}的公差为d,由
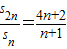
得:
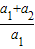
=3,所以a
2=2,即d=a
2-a
1=1,
所以a
n=n.
(Ⅱ)由b
n=a
np
an,得b
n=np
n.所以T
n=p+2p
2+3p
3+…+(n-1)p
n-1+np
n,①
当p=1时,T
n=
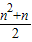
;
当p≠1时,
pT
n=p
2+2p
3+3p
4+…+(n-1)p
n+np
n+1,②
①-②得(1-p)T
n=p+p
2+p
3+…+p
n-1+p
n-np
n+1=
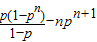
,
即T
n=
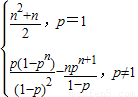
.
点评:本题主要考查对数列递推关系的观察能力和利用错位相减法求和的能力,难度中等,注意分类讨论思想的应用.

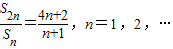 ,
,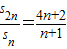 得:
得: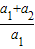 =3,所以a2=2,即d=a2-a1=1,
=3,所以a2=2,即d=a2-a1=1,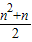 ;
;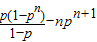 ,
,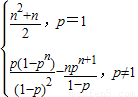 .
.
