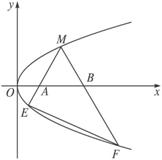
思路点拨：本题要证明直线EF的斜率为定值，不难想到这个定值与定点M有关，因此在解决过程中，不难想到先假设定点M的坐标，从而结合已知条件将其斜率表示出来得到结果.
解：设M(y02,y0)，直线ME的斜率为k(k＞0)，则直线MF的斜率为-k，方程为y-y0=k(x-y02).
由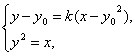
消x得ky2-y+y0(1-ky0)=0，解得yE=
∴xE=
,同理可求得yF=
,xF=
,
∴kEF=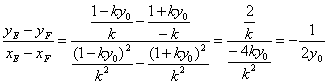
(定值)，所以直线EF的斜率为定值.
［一通百通］ 对于有关抛物线与直线的交点问题，处理的方法通常是联立直线方程与抛物线方程消去其中一个未知数，但对于具体问题来说，通常要因问题而定，如果相应的交点坐标不难解出，这时可以考虑具体找到交点坐标从而将问题解决.
科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044
如下图已知抛物线y2＝2px(p＞0)的焦点为F，A是抛物线上横坐标为4且位于x轴上方的点，A到抛物线准线的距离等于5．过A作AB垂直于y轴，垂足为B，OB的中点为M．
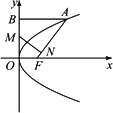
(1)求抛物线方程；
(2)求M作MN⊥FA，垂足为N，求点N的坐标；
(3)以M为圆心，MB为半径作圆M，当K(m，0)是x轴上一动点时，讨论直线AK与圆M的位置关系．
查看答案和解析>>
科目：高中数学 来源： 题型：
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴,M(0,
)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0),B(6,0)同时跟踪航天器.(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A,B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
查看答案和解析>>
科目：高中数学 来源： 题型：
=1，变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,
)为顶点的抛物线的实线部分，降落点为D(8,0).观测点A(4,0)、B(6，0)同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程；
(2)试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时.应向航天器发出变轨指令？
查看答案和解析>>
科目：高中数学 来源： 题型：
=1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,
)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
查看答案和解析>>
科目：高中数学 来源： 题型：
=1,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以y轴为对称轴、M(0,
)为顶点的抛物线的实线部分,降落点为D(8,0).观测点A(4,0)、B(6,0)同时跟踪航天器.
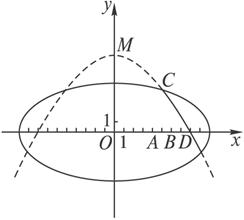
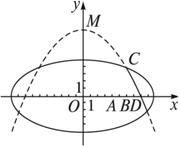
(1)求航天器变轨后的运行轨迹所在的曲线方程；
(2)试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为多少时,应向航天器发出变轨指令？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com