练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    美国与加拿大作为北美洲的代表参加了世界橄榄球比赛．美、加两国代表队夺取冠军的概率分别是和．试求北美洲在这次比赛中夺冠的概率．

    答案：19,28
    解析：

    美、加两队夺冠事件是互斥的．所以设“美夺冠”为事件A，“加夺冠”为事件B，则P(A∪B)=P(A)＋P(B)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

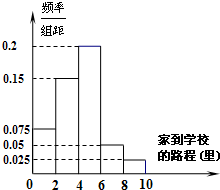    精英家教网某高中地处县城，学校规定家到学校的路程在10里以内的学生可以走读，因交通便利，所以走读生人数很多．该校学生会先后5次对走读生的午休情况作了统计，得到如下资料：
    ①若把家到学校的距离分为五个区间：[0，2）、[2，4）、[4，6）、[6，8）、[8，10），则调查数据表明午休的走读生分布在各个区间内的频率相对稳定，得到了如图所示的频率分布直方图；
    ②走读生是否午休与下午开始上课的时间有着密切的关系．下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表．
    下午开始上课时间 1：30 1：40 1：50 2：00 2：10
    平均每天午休人数 250 350 500 650 750
    （Ⅰ）若随机地调查一位午休的走读生，其家到学校的路程（单位：里）在[2，6）的概率是多少？
    （Ⅱ）如果把下午开始上课时间1：30作为横坐标0，然后上课时间每推迟10分钟，横坐标x增加1，并以平均每天午休人数作为纵坐标y，试列出x与y的统计表，并根据表中的数据求平均每天午休人数
    y
    与上课时间x之间的线性回归方程
    y
    =bx+a；
    （Ⅲ）预测当下午上课时间推迟到2：20时，家距学校的路程在6里路以上的走读生中约有多少人午休？
    （注：线性回归直线方程系数公式b=
    n
    i=1
    (xi-
    .
    x
    )(yi-
    .
    y
    )
    n
    i=1
    (xi-
    .
    x
    )    2
    =
    n
    i=1
    xiyi-n
    .
    x
    •
    .
    y
    n
    i=1
    xi2-n
    .
    x
    2
    ，a=
    .
    y
    -b
    .
    x
    ．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下表是最近十届奥运会的年份、届别、主办国，以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据：
    年份 1972 1976 1980 1984 1988 1992 1996 2000 2004 2008
    届别 20 21 22 23 24 25 26 27 28 29
    主办国家 联邦德国 加拿大 苏联 美国 韩国 西班牙 美国 澳大利亚 希腊 中国
    上届金牌数 5 0 49 未参加 6 1 37 9 4 32
    当界金牌数 13 0 80 83 12 13 44 16 6 51
    某体育爱好组织，利用上表研究所获金牌数与主办奥运会之间的关系，
    求出主办国在上届所获金牌数（设为x）与在当届所获金牌数（设为y）之间的线性回归方程
    y
    =
    b
    x+
    a
    ，其中
    b
    =1.4    ，
    在2008年第29届北京奥运会上英国获得19块金牌，则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为（所有金牌数精确到整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•上海）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题．
    例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”．求出体积
    16
    3
    后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为
    16
    3
    ，求侧棱长”；也可以是“若正四棱锥的体积为
    16
    3
    ，求所有侧面面积之和的最小值”．
    试给出问题“在平面直角坐标系xoy中，求点P（2，1）到直线3x+4y=0的距离．”的一个有意义的“逆向”问题，并解答你所给出的“逆向”问题．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    美国与加拿大作为北美洲的代表参加了世界橄榄球比赛．美、加两国代表队夺取冠军的概率分别是和．试求北美洲在这次比赛中夺冠的概率．

    查看答案和解析>>

    同步练习册答案