
已知
 为常数).
为常数).
(1)
若xÎ R,求f(x)的单调递增区间;(2)
若 时,f(x)的最大值为4,求a.
时,f(x)的最大值为4,求a. 科目:高中数学 来源:101网校同步练习 高二数学 苏教版(新课标·2004年初审) 苏教版 题型:044
已知![]() 为常数,且a≠0),f(2)=1,f(x)=x有两个相同的根
为常数,且a≠0),f(2)=1,f(x)=x有两个相同的根
(1)求f(x)的表达式;
(2)设数列{xn}满足xn+1=f(xn),且x1>0,证明![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省招生仿真卷理科数学试卷(解析版) 题型:解答题
.(本题满分15分)已知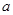 为常数,函数
为常数,函数 (
( )。
)。
(Ⅰ)
若函数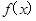 在区间(-2,-1)上为减函数,求实数
在区间(-2,-1)上为减函数,求实数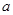 的取值范围;
的取值范围;
(Ⅱ).设
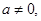 记函数
记函数 ,已知函数
,已知函数 在区间
在区间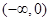 内有两个极值点
内有两个极值点 ,且
,且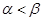 ,若对于满足条件的任意实数
,若对于满足条件的任意实数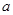 都有
都有 (
(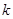 为正整数),求
为正整数),求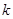 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏北四市(徐、连、淮、宿)高三元月调研测试数学试卷 题型:解答题
(本小题满分16分)设数列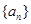 的前n项和为
的前n项和为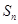 ,已知
,已知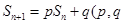 为常数,
为常数,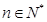 ),eg
),eg 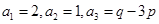
(1)求p,q的值;
(2)求数列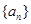 的通项公式;
的通项公式;
(3)是否存在正整数m,n,使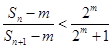 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源:广东省实验中学2009-2010学年度高一下学期考试 题型:解答题
已知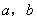 为常数,
为常数,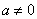 ,函数
,函数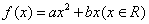 ,
,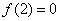 且方程
且方程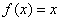 有等根.
有等根.
(1)求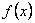 的解析式及值域;
的解析式及值域;
(2)设集合 ,
,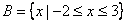 ,若
,若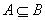 ,求实数
,求实数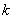 的取值范围;
的取值范围;
(3)是否存在实数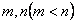 ,使
,使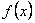 的定义域和值域分别为
的定义域和值域分别为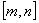 和
和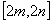 ?若存在,求出
?若存在,求出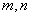 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com