
 ,AE、CF都与平面ABCD垂直,AE=1,CF=2,
,AE、CF都与平面ABCD垂直,AE=1,CF=2,
| 解:(Ⅰ)连接AC、BD交于菱形的中心O, 过O作OG⊥AF,G为垂足,连接BG、DG, 由BD⊥AC,BD⊥CF得BD⊥平面ACF,故BD⊥AF, 于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF, ∠BGD为二面角B-AF-D 的平面角, 由FC⊥AC,FC=AC=2,得  , , 由  ,得 ,得 , ,∴二面角B-AF-D的大小为  。 。 |
 |
| (Ⅱ)连EB、EC、ED,设直线AF与直线CE相交于点H, 则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD, 过H作HP⊥平面ABCD,P为垂足, 因为EA⊥平面ABCD,FC⊥平面ABCD, 所以平面ACFE⊥平面ABCD,从而  , ,由  ,得 ,得 , ,又因为  , ,故四棱锥H-ABCD的体积  。 。 |
 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010-2011学年河北省高三高考仿真理数 题型:解答题
(本小题满分12分)
如图,四棱椎P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是300,点F是PB的中点,点E在边BC上移动。
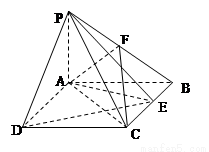
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)证明:无论点E在边BC的何处,都有AF⊥PE;
(3)求当BE的长为多少时,二面角P-DE-A的大小为450。
查看答案和解析>>
科目:高中数学 来源:0103 模拟题 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,四棱椎P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面
ABCD所成的角是300,点F是PB的中点,点E在边BC上移动。
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
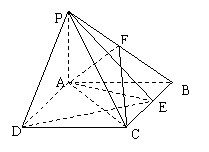 (2)证明:无论点E在边BC的何处,都有AF⊥PE;
(2)证明:无论点E在边BC的何处,都有AF⊥PE;
(3)求当BE的长为多少时,二面角P-DE-A的大小为450。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,四棱椎P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面
ABCD所成的角是300,点F是PB的中点,点E在边BC上移动。
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
 (2)证明:无论点E在边BC的何处,都有AF⊥PE;
(2)证明:无论点E在边BC的何处,都有AF⊥PE;
(3)求当BE的长为多少时,二面角P-DE-A的大小为450。
查看答案和解析>>
科目:高中数学 来源:河北省唐山一中2010高考模拟试卷(二)(理) 题型:解答题
如图,四棱椎P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面
ABCD所成的角是300,点F是PB的中点,点E在边BC上移动。
(1)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
 (2)证明:无论点E在边BC的何处,都有AF⊥PE;
(2)证明:无论点E在边BC的何处,都有AF⊥PE;
(3)求当BE的长为多少时,二面角P-DE-A的大小为450。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com