练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知空间四边形ABCD，P、Q分别是△ABC和△BCD的重心.求证：PQ∥平面ACD.

    【探究】 欲证线面平行，须证线线平行，即要证明PQ与平面ACD中的某条直线平行，根据条件，此直线为AD，如图所示.

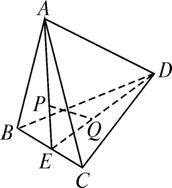
    证明：取BC的中点E，∵P是△ABC的重心，连结AE，则AE：PE=3：1，连结DE，

    ∵Q为△BCD的重心，

    ∴DE：QE=3：1，

    ∴在△AED中，PQ∥AD.

    又AD平面ACD，PQ平面ACD，

    ∴PQ∥平面ACD.

    【规律总结】 (1)本例中构造直线AD与PQ平行，是充分借助于题目的条件：P、Q分别是△ABC和△BCD的重心，借助于比例的性质证明PQ∥AD，这种方法经常使用，注意把握.

    (2)欲证线面平行，只须证线线平行，判定定理给我们提供了一种证明线面平行的方法，根据问题具体情况要熟练运用.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
    求证：
    （1）AB⊥平面CDE；
    （2）平面CDE⊥平面ABC；
    （3）若G为△ADC的重心，试在线段AE上确定一点F，使得GF∥平面CDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
    求证：（1）AB⊥平面CDE；
    （2）平面CDE⊥平面ABC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点，求证：
    （1）AB⊥平面CDE；
    （2）平面CDE⊥平面ABC；
    （3）若G为△ADC的重心，试在线段AE上确定一点F，使得GF∥平面CDE．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河南省高三12月月考文科数学卷 题型：解答题

    (本小题满分12分)

    如图，已知空间四边形ABCD中，BC=AC, AD=BD,E是AB的中点，

    求证：

    AB⊥平面CDE；

    平面CDE⊥平面ABC;

    若G为△ADC的重心，试在线段AB上确定一点F，使得GF∥平面CDE.

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
    求证：
    （1）AB⊥平面CDE；
    （2）平面CDE⊥平面ABC；
    （3）若G为△ADC的重心，试在线段AE上确定一点F，使得GF∥平面CDE．
    精英家教网

    查看答案和解析>>

    同步练习册答案