已知函数f(x)=(ax2+x)ex,其中e是自然数的底数,a∈R.
(1)当a<0时,解不等式f(x)>0;
(2)若f(x)在[-1,1]上是单调增函数,求a的取值范围;
(3)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
【答案】
分析:(1)根据e
x>0,a<0,不等式可化为
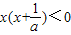
,由此可求不等式f(x)>0的解集;
(2)求导函数,再分类讨论:①当a=0时,f′(x)=(x+1)e
x,f′(x)≥0在[-1,1]上恒成立;②当a≠0时,令g(x)=ax
2+(2a+1)x+1,因为△=(2a+1)
2-4a=4a
2+1>0,f(x)有极大值又有极小值.若a>0,可得f(x)在[-1,1]上不单调;若a<0,要使f(x)在[-1,1]上单调,因为g(0)=1>0,必须满足
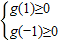
,从而可确定a的取值范围;
(3)当a=0时,原方程等价于
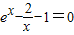
,构建函数
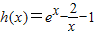
,求导函数,可确定h(x)在(-∞,0)和(0,+∞)内是单调增函数,从而可确定方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,故可得k的值.
解答:解:(1)因为e
x>0,所以不等式f(x)>0,即为ax
2+x>0,
又因为a<0,所以不等式可化为
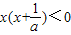
,
所以不等式f(x)>0的解集为
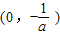
.(4分)
(2)f′(x)=(2ax+1)e
x+(ax
2+x)e
x=[ax
2+(2a+1)x+1]e
x,
①当a=0时,f′(x)=(x+1)e
x,f′(x)≥0在[-1,1]上恒成立,
当且仅当x=-1时取等号,故a=0符合要求;(6分)
②当a≠0时,令g(x)=ax
2+(2a+1)x+1,
因为△=(2a+1)
2-4a=4a
2+1>0,所以g(x)=0有两个不相等的实数根x
1,x
2,不妨设x
1>x
2,
因此f(x)有极大值又有极小值.
若a>0,因为g(-1)•g(0)=-a<0,所以f(x)在(-1,1)内有极值点,故f(x)在[-1,1]上不单调.(8分)
若a<0,可知x
1>0>x
2,因为g(x)的图象开口向下,要使f(x)在[-1,1]上单调,
因为g(0)=1>0,必须满足
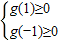
,即
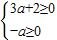
,所以
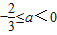
.
综上可知,a的取值范围是
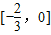
.(10分)
(3)当a=0时,方程即为xe
x=x+2,由于e
x>0,所以x=0不是方程的解,所以原方程等价于
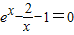
,
令
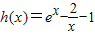
,
因为
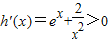
对于x∈(-∞,0)∪(0,+∞)恒成立,
所以h(x)在(-∞,0)和(0,+∞)内是单调增函数,(13分)
又h(1)=e-3<0,h(2)=e
2-2>0,
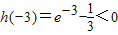
,h(-2)=e
-2>0,
所以方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,
所以整数k的所有值为{-3,1}.(16分)
点评:本题考查解不等式,考查导数知识的运用,考查函数的单调性,考查函数与方程思想,考查分类讨论的数学思想,综合性强.

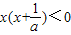 ,由此可求不等式f(x)>0的解集;
,由此可求不等式f(x)>0的解集;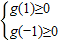 ,从而可确定a的取值范围;
,从而可确定a的取值范围;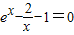 ,构建函数
,构建函数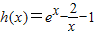 ,求导函数,可确定h(x)在(-∞,0)和(0,+∞)内是单调增函数,从而可确定方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,故可得k的值.
,求导函数,可确定h(x)在(-∞,0)和(0,+∞)内是单调增函数,从而可确定方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,故可得k的值.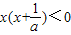 ,
,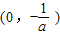 .(4分)
.(4分)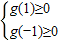 ,即
,即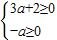 ,所以
,所以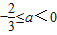 .
.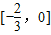 .(10分)
.(10分)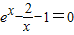 ,
,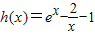 ,
,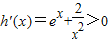 对于x∈(-∞,0)∪(0,+∞)恒成立,
对于x∈(-∞,0)∪(0,+∞)恒成立,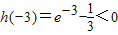 ,h(-2)=e-2>0,
,h(-2)=e-2>0,

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案